- Конструирование бутылки Клейна
- 3d принтер: «бутылка Клейна» за 82 минуты
- Интеллектуальные развлечения. Интересные иллюзии, логические игры и загадки.
- Добро пожаловать В МИР ЗАГАДОК, ОПТИЧЕСКИХ ИЛЛЮЗИЙ И ИНТЕЛЛЕКТУАЛЬНЫХ РАЗВЛЕЧЕНИЙСтоит ли доверять всему, что вы видите? Можно ли увидеть то, что никто не видел? Правда ли, что неподвижные предметы могут двигаться? Почему взрослые и дети видят один и тот же предмет по разному? На этом сайте вы найдете ответы на эти и многие другие вопросы.
- Log-in.ru© — мир необычных и интеллектуальных развлечений. Интересные оптические иллюзии, обманы зрения, логические флеш-игры.
- Интересно
- Трогаем бесконечность. Мебиус, Клейн и другие топологические парадоксы
- Односторонние поверхности : Лист Мебиуса и Бутылка Клейна
- Это древняя головоломка о трёх колодцах и трёх домах.
- Фокус №1
- Фокус №2
- Фокус №3
- Фокус№4
- ЮФокус №5
- Возникает логичный вопрос: Существуют ли ещё подобные объекты?
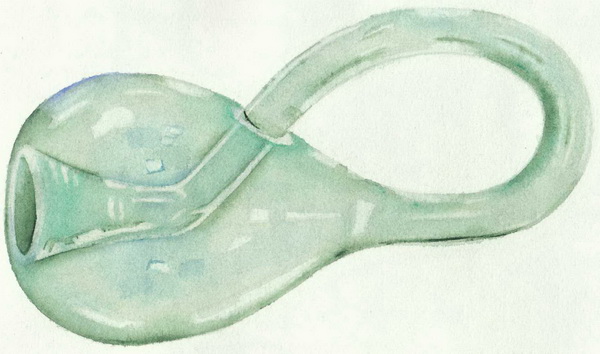
- Вот – обычная Бутылка Клейна:
- 41 комментарий
Конструирование бутылки Клейна
С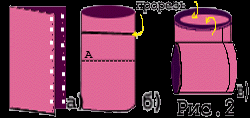
Способ № 2. Получение бутылки Клейна из стандартной пластмассовой бутылки. Необходимо взять бутылку с отверстием в донышке, вытянуть горлышко, изогнуть его вниз, и продев его через отверстие в стенке бутылки (для настоящей бутылки Клейна в четырёхмерном пространстве это отверстие не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве), присоединить к отверстию на дне бутылки.
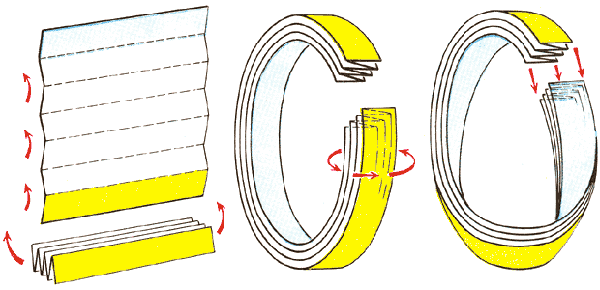
Способ № 3. Получение бутылки Клейна из одного цилиндра. Один из краёв цилиндра изгибается в обратную сторону, проходит сквозь цилиндр и склеивается с другим краем. Чтобы совершить это склеивание, необходимо исказить ширину цилиндра.
Способ № 4. Получение бутылки Клейна из ткани. Целесообразно взять кусок носка или колготок и проделать с ними то же, что и с цилиндром.
Способ № 5. Получение бутылки Клейна склеиванием двух листов Мёбиуса. Бутылка Клейна может быть получена склеиванием двух лент Мёбиуса по краю. Однако в обычном трехмерном евклидовом пространстве R 3 сделать это, не создав самопересечения, невозможно. Поэтому Бутылка Клейна не может быть вложена (только погружена) в трёхмерное евклидово пространство R 3 , но вкладывается в R 4 .
Источник
3d принтер: «бутылка Клейна» за 82 минуты
Еще неделю назад я практически ничего не знал про 3d принтеры.
Но они обладают какой-то мистической притягивающей аурой, и вот все мысли теперь только о них. (Учитывая, что дети вовсю резвятся с этими штуками, и на что способны эти девайсы.)
После недолгого гугления я нашел, где в Москве можно комфортно экспериментировать с этими штуками из будущего.
Чтобы стать мастером кунг-фу трехмерной печати, я ставлю для себя следующие этапы:
1. Напечатать «бутылку Клейна»
Под руководством опытного мастера и скачав модель с thingiverse.com
2. Самостоятельно нарисовать и самостоятельно напечатать тессеракт(проекцию гиперкуба)
3. Собрать RepRap.
4. Напечатать и собрать робота (например, Bioloid)
Итак, я приступил к реализации пункта 1.
Вот что получилось в итоге
Статистика:
Длина нити 162 метра
Время печати: 1 час 22 минуты 38 секунд
Масса пластика 11.5 г
Объем пластика 10.7 см в кубе
Ниже описал процесс по шагам
Скачав с thingiverse.com модельку я загрузил ее в программу-слайсер ReplicatorG, которая «нарезает» модель на слои.
Далее сохраняем G-code (набор управляющих команд для принтера) на SD-карту, и вставляем эту карточку в нашего красавца:
Далее принтер разогревается и начинает печатать:
Остается только сточить вспомогательные элементы и бутылка у которой нет «внутри» и «снаружи» готова.
После проделанного эксперимента остается странное ощущение «нереальности». Еду в метро, держу игрушку в руках и не верится, что я ее «создал».
Но у вас эта статья, а у меня — предмет на полочке как доказательство того, что каждый уже может материализовывать свои задумки.
А какой бы первый объект распечатали вы, будь у вас возможность?
П.С.
Кадры из к/ф «Пятый элемент»
Источник
Интеллектуальные развлечения. Интересные иллюзии, логические игры и загадки.
Добро пожаловать В МИР ЗАГАДОК, ОПТИЧЕСКИХ
ИЛЛЮЗИЙ И ИНТЕЛЛЕКТУАЛЬНЫХ РАЗВЛЕЧЕНИЙСтоит ли доверять всему, что вы видите? Можно ли увидеть то, что никто не видел? Правда ли, что неподвижные предметы могут двигаться? Почему взрослые и дети видят один и тот же предмет по разному? На этом сайте вы найдете ответы на эти и многие другие вопросы.
Log-in.ru© — мир необычных и интеллектуальных развлечений. Интересные оптические иллюзии, обманы зрения, логические флеш-игры.
Привет! Хочешь стать одним из нас? Определись 

Если ты уже один из нас, то вход тут.
Интересно
Глаз у страуса больше, чем его мозг.
Трогаем бесконечность. Мебиус, Клейн и другие топологические парадоксы
Односторонние поверхности : Лист Мебиуса и Бутылка Клейна
Мы так часто слышим слово – Бесконечность, а не хотелось ли вам когда ни будь подержать эту самую бесконечность в своих руках? Для того что бы сделать это вам придётся взять в руки бумагу, ножницы и клей. Отрежьте полоску бумаги и склейте её как показано на рисунке.
У Вас получилась такая односторонняя поверхность:
Что значит односторонняя? Это значит, что муравей (или житель Плоскатии , о котором мы говорили в предыдущей статье) побывает на обеих сторонах этого листа не переходя через край. Это значит, что вы можете не отрывая карандаша от бумаги, и не переходя через край закрасить эту фигуру с обеих сторон.
Если вам кажется что ничего особенного в этом нет, тогда попробуйте решить следующую головоломку:
Это древняя головоломка о трёх колодцах и трёх домах.
В ряд стоят 3 дома, напротив каждого из них есть по колодцу. Нужно от каждого дома сделать тропинки к каждому из колодцев так, что бы никакие 2 тропинки не пересекались.
Ниже вы можете сделать это в динамике, только колодцы тут заменены: Газом, Водой и Электричеством. Нужно к каждому из домов провести и газ и воду и электричество, и что бы ни какие 2 трубы ( электрические кабеля) не пересекались.
Ну как? Не получается?
Не так давно была доказана неразрешимость этой задачи при помощи формулы Эйлера (см. заметку на нашем сайте «Прогулка по мостам»).
Но задача эта не разрешима на ПЛОСКОСТИ, НА БУМАГЕ.
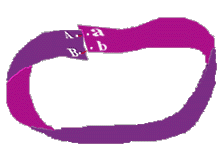
Разве мы с вами живем на бумаге? Нас со школы учили оперировать понятиями «Эвклидовой геометрией», а по простому — нас со школы учили мыслить «Плоско». Что же касается этой головоломки, то она имеет решение, только не в придуманном, а в реальном мире. В этом нам поможет Лист Мебиуса. Соедините соответствующие буквы, и получите ответ на головоломку.
Разумеется, это только начало. Лист Мебиуса таит в себе ещё много неожиданностей.
Фокус №1
Сделайте ещё один Лист Мебиуса, повёрнутый на пол оборота (180 градусов). А теперь попробуйте его разрезать посредине.
Я Вам не скажу что получится так как:
а) Если Вы уже держите в руках Лист Мебиуса и ножницы, то лишить Вас удовольствия наблюдать за тем, что произойдёт после разрезания – это просто преступление.
б) Если Вы и не думали брать в руки ножницы – тогда сказанный мною результат вас не удивит.
Ну как получилось? Обратите внимание, на сколько оборотов закручен полученный экземпляр?
Фокус №2
Закрутите Лист на 2 полуоборота(360 градусов) , и разрежьте его посередине. Что получается?
Фокус №3
Изготовьте Лист Мебиуса, который закручен на пол оборота (180 градусов), и начинайте его разрезать отступая все время одну треть от края.
Что получается на этот раз?
Фокус№4
Теперь изготовьте Лист Мебиуса, который закручен на 3 полуоборота (540 градусов), и разрежьте его пополам. У вас должен получиться Лист Мебиуса, который закручен узлом. Вроде этого, но сложнее:
ЮФокус №5
Интересные вещи так же получатся, если сложить бумагу гармошкой, затем скрутить из неё Лист Мёбиуса и резать пополам, или отступая одну треть. Первым делом сделайте гармошку, которая состоит из одного перегиба, образуйте лист Мебиуса поворотом на 360 градусов, и разрежьте посредине. Перед вами предстанут 3 сцепленных между собой кольца.
Вы делаете новые и новые Листы, а ведь не каждую полоску можно скрутить в Лист Мебиуса. Например, из квадратного листа бумаги Лист Мебиуса не получится. Тогда какое должно быть минимально отношение длины к ширине полоски, что бы из неё можно было склеить Лист Мебиуса?
Примем для ясности ширину полоски за 1. Оказывается, что минимальная длина полоски равняется v3, это приблизительно 1,73. Полученное значение равно второму «Золотому сечению».
Возникает логичный вопрос: Существуют ли ещё подобные объекты?
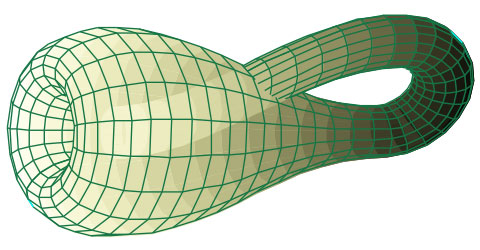
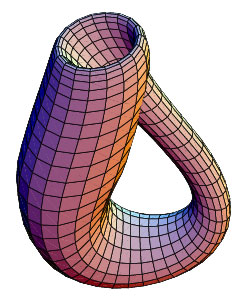
Да, существуют, и ещё более замысловатые. Если Лист Мебиуса – «условно двумерный объект» (он получен из плоской полоски), то его подружка — Бутылка Клейна полноправно занимает 3 измерения. Вот как она выглядит:
Бутылка Клейна — 3D подружка плоского Мебиуса
Запустите суда муравья, и бедняга побывает во всех точках Бутылки Клейна – не делая в ней дырок, и не переползая через край.
На всех рисунках показано следующее: в месте, где трубка «проникает в бутылку» — нет зазора, хотя это не правильно! Ведь если нет зазора, тогда муравей должен будет выползать из бутылки тем же маршрутом, каким он туда вползал. Разве бродя по Листу Мебиуса ему нужно было разворачиваться после того как он куда то дошёл? Бесконечность, она на то и бесконечность!
А почему мы только обходим Бутылку Клейна? Ведь Лист Мёбиуса мы резали вдоль и поперёк. Что же будет если разрезать Бутылку Клейна?
Это невероятно, но получился Лист Мебиуса. Резать, правда, нужно было так, что бы режущий предмет делал оборот в 360 градусов между начальной точкой и конечной.
Бутылка Клейна в трёх измерениях — это аналог Листа Мёбиуса в двух измерениях. Выше вы видели «многослойный» Лист Мебиуса — полученный склеиванием бумаги сложенной «гармошкой». А существуют ли «Многослойные» Бутылки Клейна? Как оказалось – существуют. Назовём их – Бутылки Макса (придумал автор статьи — Максим К.).
Вот – обычная Бутылка Клейна:
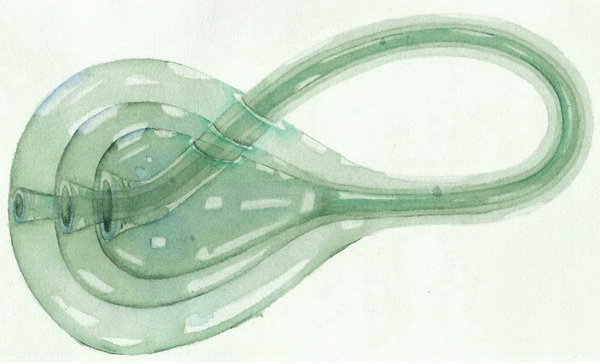
А теперь мысленно представьте себе, как внутри этой бутылки начинает формироваться новая Бутылка Клейна. Сначала внутри образуется «Бутылка Клейна» без «трубки» — бутылка с двумя отверстиями , затем образуется трубка, которая проникает в «трубку» иcходной «Бутылки Клейна», проходит всю «трубку», проникает через отверстие в только что сформировавшуюся «Бутылку Клейна». Затем трубка проникает во второе отверстие основной «Бутылки Клейна ». Находясь в задней части основной бутылки , «трубка» начинает медленно обволакивать исходную «Бутылку Клейна» превращаясь при этом в третью , самую большую «Бутылку Клейна».
Процесс доходит до «трубки» — изначальной «Бутылки Клейна» , и постепенно обволакивает её, затем эта «трубка» проникает только что сформировавшуюся «Бутылку Клейна», затем в исходную, затем в самую маленькую. Проникнув в самую маленькую «Бутылку Клейна », «трубка» доходит до отверстия и сливается с ним.
Получилось что самая маленькая «Бутылка Клейна» перешла в самую большую, и стала с ней одним целым. Ниже рисунок того, что вы пытались вообразить.
Не обязательно понимать этот мир, нужно лишь найти себя в нем – Альберт Эйнштейн
И всё же, так ли уж нужно ломать голову над тем, как устроен этот мир? Или всё что нам нужно уже есть, и нам остается лишь выбрать «правильный» вариант? Выбор как всегда за вами. Он у вас есть даже в том – делать этот выбор или нет.
По материалам: СОЗЕРЦАЕМ.COM.UA
41 комментарий
шар ( 0 )
19.12.2013 20:54
сматрите на ютубе как можно вывернуть мяч наизнанку не делая разреза. /там пахлещще мозг раком ставит/
Yury 777 ( 0 )
14.12.2013 21:31
Тема кольца Мебиуса [КМ] уже давным-давно изъезжена вдоль и поперек. Да это и не удивительно. Тысячи людей уже больше 150-ти лет восхищаются КМ и описывают его уникальные свойства. Но, фактически, никаких новых знаний о КМ с увеличением числа публикаций о нем не прибавляется. Все топчутся на одном месте, описывая одни и те же эксперименты с кольцом. rn Однако, интерес к теме не ослабевает. Видимо, загадочная сила этого необычного кольца такова, что оно, как магнит, притягивает и притягивает к себе любознательных. Каждое новое поколение открывает для себя КМ заново. Каждый хочет убедиться во всем на собственном опыте. Поэтому сам клеит, режет и удивляется. rn А недавно было выявлено, что КМ это совсем и не уникум. Что существует целая СИСТЕМА односторонних колец, и кольцо … – только одна из фигур этой системы. rn Если хотите узнать подробнее, зайдите на форум http://moebius.ucoz.com/ . Там есть статья: «Заглянуть за горизонт», в которой приведено описание всей системы односторонних колец. В этой статье, в популярной форме рассказано о том, как можно самому сделать одностороннее кольцо с любым количеством поверхностей, а не только с двумя, как у КМ. И о том, как можно предсказать свойства любого из таких колец, даже не изготавливая его в материале. rn Указанная статья — находка для преподавателей математики и возможность для нынешних школьников и студентов шагнуть дальше своих дедушек и бабушек в познании удивительных свойств односторонних фигур.rn На этом форуме есть ещё много разного интересного материала про кольцо Мебиуса. Причем большая часть материала совершенно уникальная и охватывает не только теоретические, но и возможные практические аспекты применения односторонних колец. Yury-777
aleksandr128 ( 0 )
21.11.2013 18:09
Автор рисунка «тройной бутылки Клейна» вводит читателей в заблуждение. Нельзя построить две и более взаимопараллельные односторонние поверхности. Это нонсенс. Внешняя и внутренняя бутылки суть одна змкнутая «бутылка», естественно, с двумя поверхностями. И только средняя «бутылка» является истинной бутылкой Клейна. http://moebius.ucoz.com .
катя ( 0 )
09.06.2014 08:29
aleksandr128: там ведь написано, что это рисунок того, что вы попытались себе вообразить, ане то, что должно получиться!
Источник