Диск эйлера своими руками чертежи

А ну-ка, крутаните монетку ребром на столе! Уже крутится? А перед самыьм падением она внезапно увеличит скорость вращения и резко затормозит, издавая дребезжащий звук, но не давая ни насладиться им, ни рассмотреть повнимательней процесс падения.
Упала … жаль, что не очень долго крутилась …((
Забавно? И не только вам!

Когда-то, в конце 19 столетия математиками были выведены уравнения движения для катящегося диска, затем другие уже, но столь же неутомимые математики, исследовали проблему устойчивости дисков при вращении. Движение вращающегося диска хорошо описывается уравнениями волчка в гравитационном поле.

В наше время в магазинах любому любителю «покрутить» предложат фирменную игрушку «диск Эйлера». Великолепный металлический диск с голографическими наклейками по ободу будет крутиться перед вашими глазами на зеркальной подставке, завораживая игрой цвета и звука.

Кто же был автором этой игрушки? Неужели сам Леонард Эйлер, знаменитый математик 18 века? Ведь какая-то часть его работ тоже была посвящена вращению …

В качестве игрушки вращающийся диск был впервые предъявлен зрителям Джозефом Бендиком в 90-х годах 20-го века. Проведя наблюдения за вращающейся монетой, он сумел добиться, чтобы диск вращался до 3 минут и даже более. Изобретение Дж. Бендика представляло собой плоский диск в виде хоккейной шайбы из хромированной стали с полированными скругленными краями диаметром в 3 дюйма и толщиной в ½ дюйма. Диск вращался на слегка вогнутом круглом зеркале диаметром 9 дюймов.

Конечно, вы уже сбегали в магазин сувениров и «диск Эйлера» у вас в руках! Запускаем, и пока он крутится, в уме начинают созревать идеи по поводу того, как объяснить его движение. Неистребимая тяга к знанию заставляет вас рыться в книгах, вспоминать, разбираться в теории вращательного движения.

Итак, диск Эйлера – это твердое цилиндрическое тело, имеющее единственную точку контакта с горизонтальной поверхностью, по которой он одновременно и катится, и вращается.

Интересно, что движение диска имеет две особенности: резкое увеличение частоты слышимого звука в конце вращения и внезапную остановку диска. Причем вращающийся диск никогда не теряет контакта с поверхностью.
Время вращения диска почти не зависит от того, под каким углом был закручен диск, и какова была его скорость вращения при пуске.

Вращение дисков проверяли даже в вакууме! Запускали сплошные диски, просто кольца и кольца с покрытием из тефлона. Оказывается, что отсутствие воздуха не очень сильно влияло на поведение вращающегося диска, хотя тефлоновое покрытие значительно увеличивало время вращения.
Чем быстрее вращается диск, тем он более устойчив при качении. Это явление, в котором скорость пропорциональна стабильности, характерно для спутников, вращающихся вокруг земли.
При вращении запущенный диск обладает одновременно и потенциальной и кинетической энергией. Потенциальной — за счет вертикального положения и кинетической — за счет вращения. В любой момент вращения баланс двух сил: силы тяжести и реакции опоры не дают диску упасть. И, если бы не трение и вибрации, диск вращался бы в течение очень долгого времени.

Но, как и при любом другом движении, на скорость вращения влияет затормаживающая сила трения о воздух, а также трение между диском и поверхностью. Кинетическая энергия вращения диска, потерянная в результате имеющегося трения, компенсируется за счет уменьшающейся потенциальной энергии диска. В результате центр массы диска опускается, все более приближаясь к поверхности, на которой происходит его вращение. Это увеличивает плечо момента силы между точкой контакта с поверхностью и центром массы, что приводит к росту вращающего момента. Увеличение вращающего момента постепенно меняет направление оси вращения, которая занимает все более вертикальное положение.

Диск начинает оседать, прокручиваясь на ребре. Угол наклона между диском и поверхностью становится все меньше. Скорость вращения диска возрастает. Резкому увеличению частоты вращения диска способствует тонкая прослойка воздуха между диском и поверхностью, на которой он вращается. Внутреннее трение воздуха способствует торможению монеты. При очень малом угле наклона вибрации диска и поверхности приводят к потере контакта между ними, и движение диска резко прекращается.
Хотя частота вращения увеличивается по мере падения диска, это, однако, не является главным источником нарастающего звука при падении диска. Звук образуется за счет вибрирования самого диска и поверхности, по которой он движется. Вибрации диска и поверхности приводят, в конце концов, к потере контакта между ними, а соударение диска и поверхности прекращает движение.

На первый взгляд все простенько, но что вы скажете о таких понятиях, как сингулярность, диссипация, бифуркации? А при объяснении физики движения «диска Эйлера» без них не обойтись!
Теория, описывающая движение диска, оказалась очень сложной, и учеными, занимавшимися проблемами вращения диска Эйлера, написаны серьезные научные работы, дающие математический анализ движения этой забавной игрушки.

Вот так! Наконец, вкусив тайны физики движения диска и научившись произносить «страшные слова» (сингулярность, диссипация и бифуркации), мы последний раз ставим на ребро диск Эйлера, раскручиваем его и успокоенные увиденным ( а всё оказалось именно так, как пишут именитые ученые) кладем на полку.
Неизвестное стало известным, но может быть не всё?

Любознательный человек будет поражен тем, сколько интересных задач можно решить с помощью этой маленькой игрушки.

Кто не знает, что такое турбулентность? Можно не знать этого термина, но большинство из вас испытывало внезапную тряску самолета в воздухе. Конструкторы самолетов стремятся предотвратить образования завихрений воздуха вокруг самолета при полете, т.к. на больших скоростях они отрицательно сказываются на целостности конструкции. Воздействие же гигантских атмосферных вихрей на самолет тоже может закончиться плачевно. А причем здесь диск Эйлера? Оказывается, процессы вихреобразования можно объяснить, используя теорию вращения, разработанную для дисков.

В результате исследовательских работ проведены даже аналогии между изменением звука при вращении диска и звуками «визжащих» тормозов автомобилей. Часть энергии диска на заключительном этапе вращения переходит в энергию звуковых колебаний, и то же самое происходит в тормозах при экстренном торможении автомобиля.
Вот оказывается, как много можно увидеть во вращении обыкновенной монеты, а уж тем более, если у тебя в руках такая научная игрушка, как «диск Эйлера»!

Кстати, а что похожего можно заметить в поведении скачущего по твердой поверхности шарика от пинг-понга? Но, как принято говорить в последнее время, это уже совсем другая история …

Источник

Круги Эйлера и примеры задач на логику

Круги Эйлера, на самом деле, достаточно часто встречаются в нашей жизни. Еще в младшей школе ученики начинают работать со схематическими фигурами, которые наглядно объясняют соотношения предметов и понятий.

Описание схемы кругов Эйлера

Круги Эйлера – геометрические конструкции, применяемые для упрощения восприятия логических связей между предметами, понятиями и явлениями.

Делятся на группы, в зависимости от типа отношений между множествами:

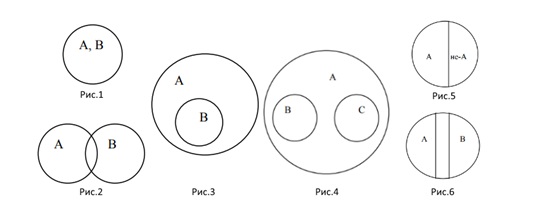
равнозначные (рис.1);
пересекающиеся (рис.2);
подчиненные (рис.3);
соподчиненные (рис.4);
противоречащие (рис.5);
противоположные (рис.6).

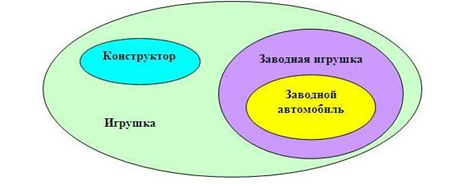
Типовой пример такой диаграммы:

Наибольшее множество, отмеченное зеленым цветом, представляет собой все варианты игрушек.

Одним из вариантов игрушек являются конструкторы. Они выделены голубым овалом. Конструкторы являются отдельным множеством, и, одновременно, частью множества «Игрушки».

Заводные игрушки также являются частью множества «Игрушки», но не относятся к множеству «Конструкторы». Поэтому, они выделяются фиолетовым овалом. А вот множество «Заводных автомобилей» является самостоятельным, но при этом, является подмножеством «Заводных игрушек».

При помощи этого метода ученый решал сложнейшие математические задачи. Применение простых фигур позволяло свести решение любой, даже самой сложной задачи, к символической логике – максимальному упрощению рассуждений.

Позже, данный способ был доработан англичанином Джоном Венном, который ввел понятие пересечения нескольких множеств.

Методика очень проста в использовании — круги Эйлера для дошкольников от 4-5 лет начинают преподавать уже в детском саду. При этом, она же на столько удобна, что применяется даже в высшей академической среде.

Применение кругов Эйлера

Основная цель использования диаграмм – практическое решение задач по объединению или пересечению множеств.

Области применения: математика, логика, менеджмент, статистика, информатика и др. На самом деле, их значительно больше, но перечислить все попросту невозможно.

Диаграммы делятся на два вида.

Первый описывает объединение понятий, вложенность одного в другое. Пример приведен в статье выше.

Второй описывает пересечения двух разных множеств некоторыми общими признаками. Один из примеров

Примеры задач и решения

Рассмотрим задачи, в которых помогают разбираться круги Эйлера, примеры решения задач по логике и математике.

Задачи для дошкольников

Первые в очереди: круги Эйлера для дошкольников, задания с ответами на которые помогут понять, как малыши впервые знакомятся с методикой упрощения сложных математических и логических задач.

Задание №1 – начальный уровень.

Цель: научить ребенка определять предмет, наиболее соответствующий одновременно двум свойствам.

Правильный ответ: кубик Рубика.

Задание №2

Правильный ответ: лягушка.

Задание №3

Правильный ответ: груша.

Задание №4 – средний уровень.

Задания усложняются тем, что используется больше множеств.

Правильный ответ: Солнце.

Задание №5

Правильный ответ: платье.

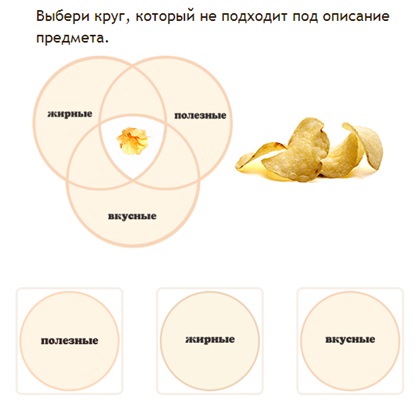
Задание №6

Правильный ответ: полезные.

Задания для школьников

Следующие задачи по логике с ответами, круги Эйлера в которых являются основой для решения, касаются младших школьников. Подобные задания обучают детей разбирать логические пересечения по определенным признакам.

Задание №1

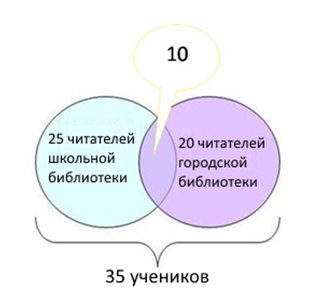
35 учеников зарегистрированы в школьной или городской библиотеках. Из них 25 регулярно посещают школьную библиотеку, а 20 – городскую.

Посещают обе библиотеки?
Не посещают городскую библиотеку?
Не посещают школьную библиотеку?
Ходят только в городскую библиотеку?
Ходят только в школьную библиотеку?

Ответ:

Определим количество посетителей двух библиотек – общая часть на диаграмме:

Ученики, не посещающие городскую библиотеку:

35 – 20 = 15 – левая сектор голубой зоны.

Ученики, не посещающие школьную библиотеку:

35 – 25 = 10 – правый сектор фиолетовой.

Посетители только городской библиотеки:

35 – 25 = 10 – также, правый сектор фиолетовой.

Посетители только школьной библиотеки:

35 – 20 = 15 – также, левый сектор голубой.

Задание №2 – также предназначено для младших классов, но является более сложным.

В 7-А учится 38 человек. Ученики увлекаются разными спортивными играми: 16 – баскетболом, 17 – хоккеем, 18 – футболом. Одновременно баскетбол и хоккей любят 4 человека, баскетбол и футбол – 3, хоккей и футбол – 5, а 3 ученика не интересуются спортом.

Есть ли ученики, увлекающиеся всеми спортивными играми?
Какое количество школьников интересуется только одной из спортивных игр?

Ответ:

Все ученики класса – наибольшая окружность.

Круг «Б» — баскетболисты, «Х» — хоккеисты, «Ф» — футболисты, «Z» — универсальные спортсмены. Трое неспортивных учеников просто находятся в общем круге.

Баскетболисты, входящие в множество «Б», но не входящие в зоны пересечения со множествами «Х» и «Ф».

16 – (4 + Z + 3) = 9 – Z.

По аналогии, находим количество хоккеистов.

17 – (4 + Z + 5) = 8 – Z.

18 – (3 + Z + 5) = 10 – Z.

Чтобы пределить значение Z, нужно суммировать множества учеников.

3 + (9 – Z) + (8 – Z) + (10 – Z) + 3 + 4 + 5 + Z = 38;

Соответственно, Б = 7, Ф = 8, Х = 6.

Применение круговых диаграмм позволяет наглядно продемонстрировать все взаимоотношения разных групп учеников.

Метод схематического изображения взаимоотношений множеств – не просто увлекательная вещь. Круги Эйлера, примеры решения задач, логика которых неочевидна, показывают, что метод может использоваться не только при развязывании математических заданий, но и находить выход из житейских ситуаций.

Источник

Кручу-верчу, запутать хочу: углы Эйлера и Gimbal lock

Выставите любой палец левой руки вперед. Давайте, не стесняйтесь, никто не будет над вами смеяться. Это нужно для важного эксперимента. Выставили? Теперь представьте что вы — это ваш палец (ну и бред). Повернитесь под прямым углом направо, затем наверх, и наконец налево. Где вы оказались? Правильно, в том же месте, но уже на спине.

С некоторой натяжкой именно так работает вращение с помощью углов Эйлера. Немного непредсказуемо и неудобно, не правда ли? Углы Эйлера имеют несколько недостатков, но есть одно особенно нехорошее свойство из-за которого вы не захотите с ними связываться. Его имя — Gimbal lock.

В русском языке gimbal lock называют по-разному: шарнирный замок, блокировка осей, складывание рамок. К сожалению, по запросам в поисковике с такими ключевыми словами выдаётся много мусора, а статья в Википедии оставляет желать лучшего, поэтому я сам расскажу вам об этом феномене и предложу как с ним бороться.

Внимание! Заходя под кат вы подвергаетесь риску поломать голову.

Для начала напомню что такое углы Эйлера. Вы наверное помните, что это что-то вроде набора из трёх углов вращения вокруг осей X, Y и Z? Не совсем так. Предположим, вы хотите повернуть некий объект, и у вас есть набор конечных углов (X: 45°, Y: 45°, Z: 45°). Один из подвохов эйлеровых углов — необходимость выбора какого-то одного порядка поворотов. Если сначала повернуть на 45° вокруг оси X, затем вокруг Y и в конце вокруг Z, то получится результат как на левой половине картинки снизу. Если порядок будет Z-X-Y, то результат будет другой, как на правой половинке.

От выбора порядка поворотов зависит место появления шарнирного замка. Что же это такое? Возьмём к примеру такой порядок поворотов: Z-X-Y. Если вращение вокруг оси X будет равно 90° или -90°, то вращения вокруг Z и Y будут «есть» друг друга и останется только огрызок от большего из вращений. Например (X: 90°, Y: 90°, Z: 90°) превратится в просто (X: 90°, Y: 0°, Z: 0°). Внимание на иллюстрацию.

Так же можно подставить (X: 90°, Y: 130°, Z: 140°) или (X: 90°, Y: 30°, Z: 40°), но в результате всё равно будет получаться (X: 90°, Y: 0°, Z: 10°). Немного не интуитивно, вам не кажется? Это всё из-за шарнирного замка. Когда вращение вокруг оси X становится равным 90° или -90°, ещё не использованная локальная ось вращения Y становится параллельной оси Z, но с обратным направлением, поэтому вращение вокруг неё вступает в конфликт с предыдущим вращением вокруг Z.

Это взорвались головы особо впечатлительных читателей. Поясню то же самое со стрелочками.

Когда оси совпадают, теряется одна степень свободы. Это и есть шарнирный замок. Вы хотите сделать поворот, но у вас не хватает осей, чтобы его осуществить.

Шарнирный замок появляется в середине иерархии поворотов. Если использовать порядок X-Y-Z или Z-Y-X, то поворот направо или налево будет заклинивать анимацию. Поскольку такой поворот встречается гораздо чаще чем, например, поворот в сторону зенита или надира, то во многих программах используют последовательность Z-X-Y. Такая иерархия поворотов используется в Unity3d, правда внутри все вращения всё равно хранятся в кватернионах. Что такое кватернионы? Об этом лучше рассказать отдельно. Кватернионы и матрицы вращения это один из способов избежать шарнирного замка. Также существуют хитрые алгоритмы, которые плавно обходят замок стороной, но это отражается на качестве анимации. Лучше всего использовать углы Эйлера только для простых случаев: пропеллеры, колёса, маятники. Иногда можно поменять иерархию поворотов, но тогда всё равно придётся помнить о замке.

По ссылкам ниже можете посмотреть интерактивную демонстрацию шарнирного замка на примере гироскопа. С ним понять иерархию поворотов и ситуации с замком намного проще.

Мышкой вращать сцену, Esc — выход, остальные кнопки указаны на экране.

Для пользователей Linux:
Сделайте файл GimbalLock исполняемым с помощью «chmod +x GimbalLock» и запускайте.

Источник