Двойной маятник своими руками

Двойной маятник своими руками

Двойной маятник — это, несомненно, настоящее чудо природы. Поразителен скачок сложности, который наблюдается при переходе от простого одиночного маятника к двойному. Колебания простого маятника имеют регулярный характер. При малых отклонениях от равновесия такие колебания являются гармоническими и описываются функцией синус или косинус. В случае нелинейных колебаний период зависит от амплитуды, но регулярность движения сохраняется. Другими словами, в случае простого маятника приближение малых колебаний вполне отражает существенные свойства системы.

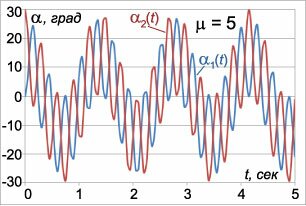
Двойной маятник «ведет себя» совершенно иначе. Уже в режиме малых колебаний у двойного маятника возникает такое новое явление как эффект биений . А при увеличении энергии характер колебаний маятников меняется принципиально − колебания становятся хаотическими . Несмотря на то, что двойной маятник можно описать системой нескольких обыкновенных дифференциальных уравнений, то есть вполне детерминированной моделью, появление хаоса выглядит очень необычно. Данная ситуация напоминает систему Лоренца , где детерминированная модель из трех уравнений также демонстрирует хаотическое поведение. Попробуйте поэкспериментировать с приведенным ниже приложением и понаблюдайте за движением двойного маятника при различных отношениях масс тел и начальных углах.

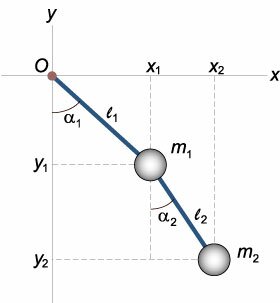
В лагранжевой механике для описания системы используются обобщенные координаты и обобщенные скорости . В нашем случае в качестве таких переменных можно взять углы отклонения маятников \(<\alpha _1>,<\alpha _2>\) и угловые скорости \(<\dot \alpha _1>,<\dot \alpha _2>.\) Используя указанные переменные, построим лагранжиан двойного маятника и запишем дифференциальные уравнения Лагранжа.

Упрощенная модель двойного маятника показана на рисунке \(1.\) Будем считать стержни невесомыми. Их длины равны \(\) и \(.\) Массы точечных тел (они представлены шарами конечного радиуса) составляют \(\) и \(.\) В точках подвеса трение отсутствует.

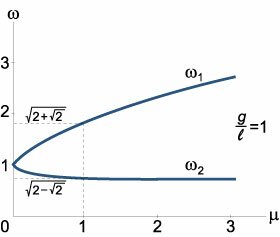
Если считать углы \(<\alpha _1>\left( t \right),<\alpha _2>\left( t \right)\) малыми, то колебания маятников вблизи нулевого положения равновесия можно описать линейной системой уравнений. Чтобы получить такую систему, вернемся назад к исходному лагранжиану системы: \[ = <\left( <\frac<<>> <2>+ \frac<<>><2>> \right)l_1^2\dot \alpha _1^2 > + <\frac<<>><2>l_2^2\dot \alpha _2^2 > + <<\dot \alpha _1><\dot \alpha _2>\cos \left( <<\alpha _1>— <\alpha _2>> \right) > + <\left( <+ > \right)g\cos <\alpha _1>> + <g\cos <\alpha _2>.> \] Запишем этот лагранжиан в более простом виде, раскладывая его в ряд Маклорена и сохраняя линейные и квадратичные члены. Тригонометрические функции можно заменить следующими приближенными выражениями: \[ <\cos <\alpha _1>\approx 1 — \frac<<\alpha _1^2>><2>,>\;\; <\cos <\alpha _2>\approx 1 — \frac<<\alpha _2^2>><2>,>\;\; <\cos \left( <<\alpha _1>— <\alpha _2>> \right) \approx 1 — \frac <<<<\left( <<\alpha _1>— <\alpha _2>> \right)>^2>>> <2>\approx 1.> \] Здесь мы учли, что слагаемое с \(\cos \left( <<\alpha _1>— <\alpha _2>> \right)\) содержит произведение малых величин \(<<\dot \alpha >_1><<\dot \alpha >_2>\) и имеет второй порядок малости. Поэтому в разложении косинуса можно ограничиться линейным членом.

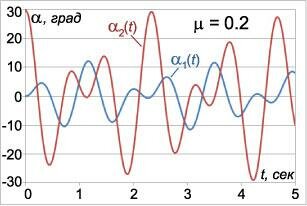
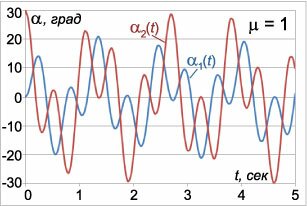
Рассмотрим характер малых колебаний для некоторого конкретного набора начальных данных. Пусть, например, координаты и скорости маятников в начальный момент имеют такие значения: \[ <<\alpha _1>\left( \right) = 0,\;\;<\alpha _2>\left( \right) = \frac<\pi ><6>,>\;\; <<\dot \alpha _1>\left( \right) = 0,\;\;<\dot \alpha _2>\left( \right) = 0.> \] В этом случае начальные фазы равны нулю: \( <\varphi _1>= <\varphi _2>= 0.\) Определим постоянные \(\) и \(:\) \[ <\left\< \begin <\alpha _1>\left( 0 \right) = + = 0\\ <\alpha _2>\left( 0 \right) = — \sqrt <\frac<<1 + \mu >><\mu >> + \sqrt <\frac<<1 + \mu >><\mu >> = \frac<\pi > <6>\end \right.,>\;\; <\Rightarrow = — ,>\;\; <\Rightarrow 2\sqrt <\frac<<1 + \mu >><\mu >> = \frac<\pi ><6>,>\;\; <\Rightarrow = \frac<\pi ><<12>>\sqrt <\frac<\mu ><<1 + \mu >>> ,>\;\; <\Rightarrow = — \frac<\pi ><<12>>\sqrt <\frac<\mu ><<1 + \mu >>> .> \] Тогда закон колебаний маятников выражается формулами \[ <<\alpha _1>\left( t \right) = — \frac<\pi ><<12>>\sqrt <\frac<\mu ><<1 + \mu >>> \cos \left( <<\omega _1>t> \right) > + <\frac<\pi ><<12>>\sqrt <\frac<\mu ><<1 + \mu >>> \cos \left( <<\omega _2>t> \right),> \] \[<\alpha _2>\left( t \right) = \frac<\pi ><<12>>\cos \left( <<\omega _1>t> \right) + \frac<\pi ><<12>>\cos \left( <<\omega _2>t> \right),\] где циклические частоты определяются соотношением \[<\omega _<1,2>> = \sqrt <\frac> \sqrt <1 + \mu \pm \sqrt <\left( <1>\right)\mu > > .\] Здесь углы \(<\alpha _1>\left( t \right),\) \(<\alpha _2>\left( t \right)\) выражаются в радианах, а время \(t\) − в секундах. На рисунках \(3-5\) приведены графики малых колебаний маятников для трех значений \(\mu:\) \( <\mu _1>= 0.2,\) \( <\mu _2>= 1,\) \( <\mu _3>= 5,\) при условии \(l = = = 0.25\,\text<м>,\) \(g = 9.8\large\frac<\text<м>><<<\text<с>^2>>>\normalsize.\) Углы отклонения маятников для удобства приведены в градусах. Из графиков видно, что в системе происходят биения , при которых энергия циклически переходит от одного маятника к другому. Когда один маятник почти останавливается, другой раскачивается с максимальной амплитудой. Через некоторое время маятники «меняются ролями» и так далее. Колебания с большей частотой \(<\omega _1>\) модулируются более низкочастотными колебаниями с частотой \(<\omega _2>.\) Это особенно хорошо заметно на рисунке \(5\) при большом значении \(\mu\) (\( <\mu _3>= 5\)), когда разница между частотами \(<\omega _1>\) и \(<\omega _2>\) велика.

Вернемся теперь снова к исходной нелинейной системе уравнений и исследуем характер колебаний с произвольной амплитудой. Такая система уравнений не решается аналитически. Поэтому мы будем рассматривать численную модель двойного маятника.

Приведенные выше уравнения Лагранжа являются дифференциальными уравнениями второго порядка. Их удобнее преобразовать в форму канонических уравнений Гамильтона . В результате вместо \(2\) уравнений второго порядка мы получим систему \(4\) дифференциальных уравнений первого порядка.

В гамильтоновой механике состояние системы определяется обобщенными координатами и обобщенными импульсами . В нашем случае в качестве обобщенных координат мы снова, как и в уравнениях Лагранжа, будем использовать углы \(<\alpha _1>,<\alpha _2>.\) Вместо обобщенных скоростей \(<\dot \alpha _1>,<\dot \alpha _2>\) (в лагранжиане) введем теперь обобщенные импульсы \(,,\) связанные со скоростями формулами \[ = \frac<<\partial L>><<\partial <<\dot \alpha >_1>>>,\;\; = \frac<<\partial L>><<\partial <<\dot \alpha >_2>>>\] или в краткой записи: \[ = \frac<<\partial L>><<\partial <<\dot \alpha >_i>>>,\;\;i = 1,2.\] Переход от лагранжевой к гамильтоновой форме уравнений производится с помощью преобразования Лежандра , которое определяется следующим образом.

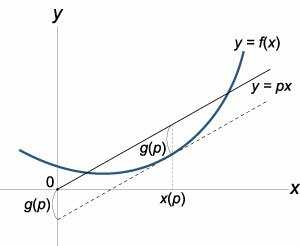
Предположим, что \(f\left( x \right)\) − гладкая выпуклая вниз функция (рисунок \(6\)). Рассмотрим прямую \(y = px,\) проходящую через начало координат. Расстояние между прямой \(y = px\) и функцией \(y = f\left( x \right)\) вдоль оси \(Oy\) зависит от координаты \(x.\) При определенном значении \(x\) это расстояние будет максимальным. Ясно, что оно зависит от наклона прямой, т.е. от параметра \(p.\) Таким образом мы вводим новую функцию \(g\left( p \right):\) \[g\left( p \right) = \max\limits_x \left( \right).\] Такое преобразование функции \(f\left( x \right)\) в сопряженную функцию \(g\left( p \right)\) называется преобразованием Лежандра . Заметим, что функция \(g\left( p \right)\) достигает максимального значения по переменной \(x\) когда \(p = \large\frac<><>\normalsize.\) Действительно, \[ <\frac<>\left( \right) = p — \frac<><> = 0,>\;\; <\Rightarrow p = \frac<><> = p\left( x \right).> \] Зная зависимость \(p\left( x \right),\) можно найти обратную функцию \(x\left( p \right).\) Тогда преобразование Лежандра будет выражаться соотношением \[g\left( p \right) = px\left( p \right) — f\left( \right),\;\;\text<где>\;\;p = \frac<><>.\] Преобразование Лежандра легко обобщается на случай функций нескольких переменных. В модели двойного маятника переход от функции Лагранжа к функции Гамильтона описывается преобразованием Лежандра в форме: \[ ,<\alpha _2>,,> \right) > = <\sum\limits_^2 <<<\dot \alpha >_i>> — L\left( <<\alpha _1>,<\alpha _2>,<<\dot \alpha >_1>,<<\dot \alpha >_2>> \right) > = <<\dot \alpha _1> + <\dot \alpha _2> — L\left( <<\alpha _1>,<\alpha _2>,<<\dot \alpha >_1>,<<\dot \alpha >_2>> \right),>\;\; <\text<где>\;\; = \frac<<\partial L>><<\partial <<\dot \alpha >_1>>>,\; = \frac<<\partial L>><<\partial <<\dot \alpha >_2>>>.> \] В этом выражении \(L\) является лагранжианом, а функция \(H\) представляет собой гамильтониан системы, который зависит от обобщенных координат \(<\alpha _1>,<\alpha _2>\) и обобщенных импульсов \(,.\)

Наиболее распространенным методом численного решения дифференциальных уравнений является метод Рунге-Кутты \(4\)-го или \(5\)-го порядка точности. Различные вариации этого метода используются в большинстве математических пакетов (MatLab, Maple, Mathematica, Mathcad), как правило, с автоматическим контролем точности и адаптивным временным шагом.

Читайте также:  Детская для новорожденного мальчика своими руками

Для моделирования движения двойного маятника мы также воспользуемся классическим методом Рунге-Кутты \(4\)-го порядка точности. Предварительно несколько упростим дифференциальные уравнения, полагая, что длины маятников одинаковы: \( = = l.\) Введем также параметр \(\mu,\) равный отношению массы второго маятника к массе первого: \(\mu = \large\frac<<>><<>>\normalsize.\) Тогда система уравнений принимает следующий вид: \[\left\< \begin <<\dot \alpha >_1> = \frac <<— \cos \left( <<\alpha _1>— <\alpha _2>> \right)>><<\left[ <1 + \mu \,<\sin^2>\left( <<\alpha _1>— <\alpha _2>> \right)> \right]>>\\ <<\dot \alpha >_2> = \frac<<\left( <1 + \mu>\right) — \mu \cos \left( <<\alpha _1>— <\alpha _2>> \right)>><<\left[ <1 + \mu \,<\sin^2>\left( <<\alpha _1>— <\alpha _2>> \right)> \right]>>\\ <<\dot p>_1> = — \left( <1 + \mu>\right)g\sin <\alpha _1>— + \\ <<\dot p>_2> = — \mu gl\sin <\alpha _2>+ — \end \right.,\] где \[ = \frac<<\sin \left( <<\alpha _1>— <\alpha _2>> \right)>><<\left[ <1 + \mu \,<<\sin>^2>\left( <<\alpha _1>— <\alpha _2>> \right)> \right]>>,\] \[ = \frac<<\left[ \mu \cos \left( <<\alpha _1>— <\alpha _2>> \right) + p_2^2\left( <1 + \mu>\right)> \right]\sin \left[ <2\left( <<\alpha _1>— <\alpha _2>> \right)> \right]>><<2<<\left[ <1 + \mu \,<<\sin>^2>\left( <<\alpha _1>— <\alpha _2>> \right)> \right]>^2>>>.\] Данную систему можно переписать в векторной форме: \[ <\mathbf= \mathbf\left( \mathbf \right),>\;\; <\text<где>\;\;\mathbf = <\left( <<\alpha _1>,<\alpha _2>,,> \right)^T>,>\;\; <\mathbf= <\left( <,,,> \right)^T>.> \] Вектор \(\mathbf\) составлен из \(4\)-х канонических переменных данной системы, а компоненты вектора \(\mathbf\) соответствуют правым частям дифференциальных уравнений.

Метод Рунге-Кутты предполагает на каждом шаге последовательное вычисление четырех промежуточных векторов: \[ <<\mathbf_1> = \tau \mathbf\left( <<\mathbf_n>> \right),>\;\; <<\mathbf_2> = \tau \mathbf\left( <<\mathbf_n> + \frac<1><2><\mathbf_1>> \right),>\;\; <<\mathbf_3> = \tau \mathbf\left( <<\mathbf_n> + \frac<1><2><\mathbf_2>> \right),>\;\; <<\mathbf_4> = \tau \mathbf\left( <<\mathbf_n> + <\mathbf_3>> \right).> \] Значение вектора \(<\mathbf_>\) в следующем временном узле вычисляется по формуле \[<\mathbf_> = <\mathbf_n> + \frac<1><6>\left( <<\mathbf_1> + 2<\mathbf_2> + 2<\mathbf_3> + <\mathbf_4>> \right).\] Суммарная ошибка данного алгоритма на конечном интервале имеет порядок \(O\left( <<\tau ^4>> \right),\) т.е. точность вычислений возрастает в \(16\) раз при уменьшении временного шага \(\tau\) в два раза.

Описанная модель реализована в анимации, приведенной в начале web-страницы. Для упрощения мы положили начальные углы отклонения маятников равными: \( <\alpha _1>= <\alpha _2>= \alpha .\) Данное приложение наглядно демонстрирует хаотическую динамику двойного маятника при различных значениях параметров \(\mu\) и \(\alpha.\) Интересно, что в некоторых режимах в системе возникают устойчивые траектории, как, например, на рисунке \(7,\) или компактные области притяжения, в которых маятник может пребывать продолжительное время (рисунок \(8\)). Похоже, что двойной маятник еще не полностью изучен физиками и математиками и таит в себе много неожиданностей.

Источник

Документация

Анимация и решение двойного движения маятника

Этот пример показывает, как смоделировать движение двойного маятника при помощи MATLAB® и Symbolic Math Toolbox™.

Решите уравнения движения двойного маятника и создайте анимацию, чтобы смоделировать двойное движение маятника.

Шаг 1: задайте смещение, скорость и ускорение двойных масс маятника

Следующие данные показывают модель двойного маятника. Двойной маятник состоит из двух маятников, качается и два твердых стержня.

Опишите движение двойного маятника путем определения переменных состояния:

угловое положение первого боба θ 1 ( t )

угловое положение второго боба θ 2 ( t )

Опишите свойства двойного маятника путем определения переменных:

длина первого стержня L 1

длина второго стержня L 2

масса первого боба m 1

масса второго боба m 2

гравитационная константа g

Для простоты проигнорируйте массы двух твердых стержней. Задайте все переменные при помощи syms .

Задайте смещения двойного маятника в Декартовых координатах.

Найдите скорости путем дифференциации смещений относительно времени с помощью функции diff .

Читайте также:  Замена передних подшипников ваз 2107 своими руками

Найдите ускорения путем дифференциации скоростей относительно времени.

Шаг 2: определите уравнения движения

Определите уравнения движения на основе законов Ньютона.

Во-первых, задайте силу первого стержня как T 1 , и сила второго стержня T 2 .

Затем, создайте схемы свободного тела сил, которые действуют на обе массы.

Оцените силы, действующие на m 1 . Определите уравнения движения первого боба путем балансировки горизонтальных и вертикальных компонентов силы. Задайте эти два уравнения как символьные уравнения eqx_1 и eqy_1 .

Оцените силы, действующие на m 2 . Определите уравнения движения второго боба путем балансировки горизонтальных и вертикальных компонентов силы. Задайте эти два уравнения как символьные уравнения eqx_2 и eqy_2 .

Шаг 3: оцените силы и уменьшайте системные уравнения

Четыре уравнения движения описывают кинематику двойного маятника. Оцените силы, действующие на стержни, и уменьшайте набор четырех уравнений к двум уравнениям.

Уравнения движения имеют четыре неизвестные: θ 1 , θ 2 , T 1 , и T 2 . Оцените эти два неизвестные T 1 и T 2 от eqx_1 и eqy_1 . Используйте функцию solve , чтобы найти T 1 и T 2 .

Замените решениями T 1 и T 2 в eqx_2 и eqy_2 .

Эти два приведенных уравнения полностью описывают движение маятника.

Шаг 4: решите системные уравнения

Решите системные уравнения, чтобы описать движение маятника.

Во-первых, задайте значения для масс в kg , длины стержня в m , и сила тяжести в m / s 2 (Единицы СИ). Замените этими значениями в эти два приведенных уравнения.

Эти два уравнения являются нелинейными дифференциальными уравнениями второго порядка. Чтобы решить эти уравнения, преобразуйте их в дифференциальные уравнения первого порядка при помощи функции odeToVectorField .

Элементы векторного V представляют дифференциальные уравнения первого порядка, которые равны производной времени элементов S . Элементы S являются переменными состояния θ 2 , d θ 2 / dt , θ 1 , и d θ 1 / dt . Переменные состояния описывают угловые смещения и скорости двойного маятника.

Затем, преобразуйте дифференциальные уравнения первого порядка в функцию MATLAB с указателем M .

Задайте начальные условия переменных состояния как [pi/4 0 pi/6 0] . Используйте функцию ode45 , чтобы решить для переменных состояния. Решения являются функцией времени в интервале [0 10] .

Постройте решения переменных состояния.

Шаг 5: создайте анимацию колеблющегося двойного маятника

Создайте анимацию колеблющегося двойного маятника.

Во-первых, создайте четыре функции, которые используют deval , чтобы оценить координаты обоих маятников из решений sols .

Затем, создайте объект Animation движения остановки первого боба маятника при помощи функции fanimator . По умолчанию fanimator создает объект Animation с 10 сгенерированными кадрами в единицу времени в области значений t от 0 до 10. Постройте координаты при помощи функции plot . Установите ось X и ось Y быть равной длиной.

Затем, добавьте объекты Animation первого твердого стержня, второго боба маятника и второго твердого стержня.

Добавьте часть текста, чтобы считать прошедшее время при помощи функции text . Используйте num2str , чтобы преобразовать параметр времени в строку.

Используйте команду playAnimation , чтобы проигрывать анимацию двойного маятника.

Документация Symbolic Math Toolbox

Поддержка

© 1994-2019 The MathWorks, Inc.

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

3. Сохраняйте структуру оригинального текста — например, не разбивайте одно предложение на два.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.

Источник