Геокупол своими руками калькулятор

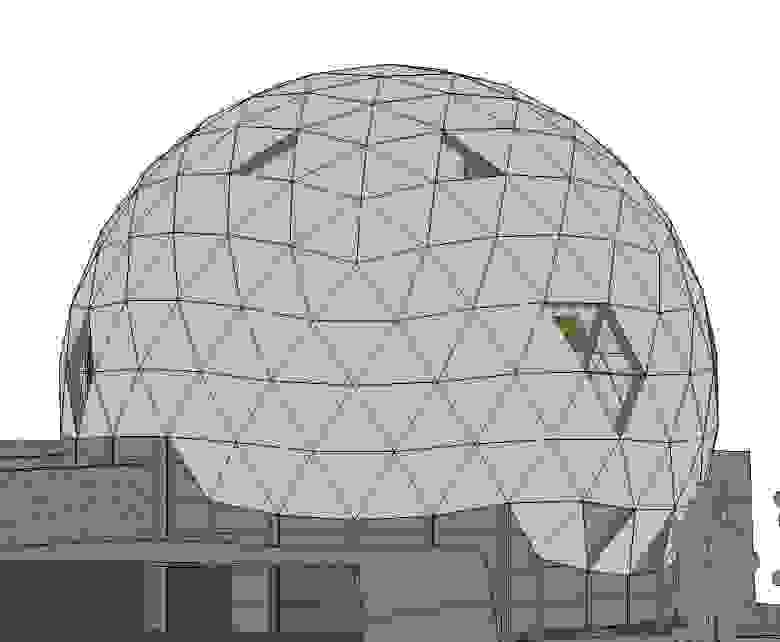
Геодезический купол. Об устройстве и моем опыте расчетов

Пожалуй сложно назвать геодезические купола чем-то необычным или новым. В этой заметке я расскажу немного об этих конструкциях в общем, об их устройстве, а также покажу на примере как я кое что на эту тему считал. Код тоже будет.

Википедию цитировать не буду. Почему я выбрал купол в качестве дома?

• При равном объеме площадь поверхности сферы будет меньше, чем у любой другой формы. Это положительно влияет как на материалоемкость, так и на энергозатраты при эксплуатации.
• Мне нравится как выглядит сфера.
• Это интересный инженерный проект, в каком-то смысле даже вызов. Это сложно, трудно и потому весело!

Как это геодезические сферы устроены вообще? С первого взгляда кажется, что это какое-то переплетение рёбер и уловить систему сложно. В этой заметке попробуем разобраться.

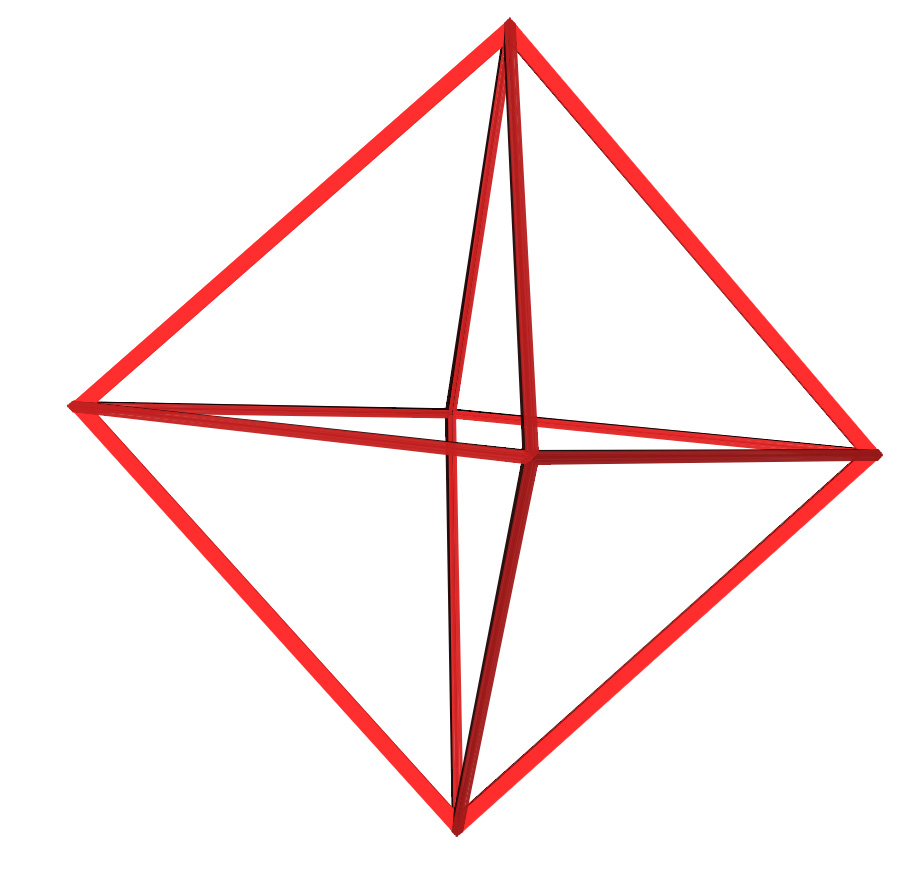
В основе таких конструкций лежит икосаэдр или октаэдр. В общем правильный многогранник.
В моем случае это был именно икосаэдр и чаще используют его. Далее берем одну грань и заменяем ее на несколько треугольников, вершины которых лежат на сфере, центр которой совпадает с центром икосаэдра. Звучит не слишком складно. Отвлечемся.

Есть замечательный калькулятор www.acidome.ru который позволяет в реальном времени покрутить геодезик. Берем в качестве основы icosahedron, ставим частоту 1, часть сферы 1/1.

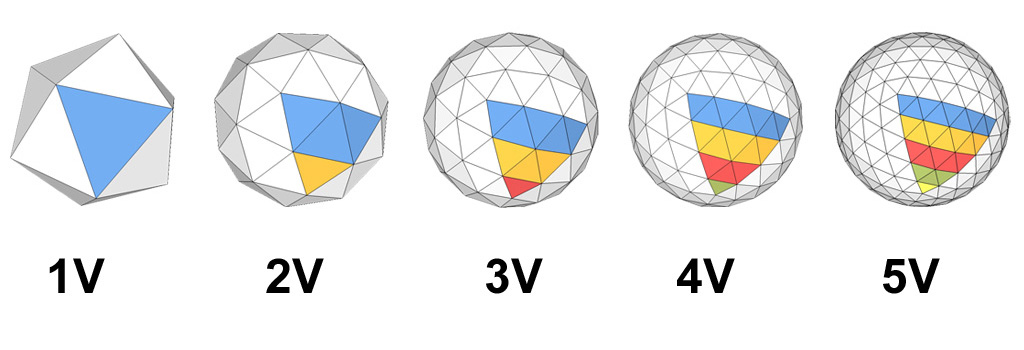
Это и есть наш основной икосаэдр. Частота это на сколько частей мы разобьем каждое ребро икосаэдра. Ставим 3,4, 5 и ничего становится непонятно. Переключаем в режим кровли и ищем пятиугольники. В тех местах, где у нас вершина икосаэдра — будет пятиугольник. Между тремя пятиугольниками грань икосаэдра.

Если внимательно смотреть на геодезик и знать, что искать (обычно пятиугольник), то становится видна регулярность структуры. На Биосфере в Монреале при должном усердии можно найти пятиугольники и посчитать частоту. Частота у нас равна количеству ребер между двумя пятиугольниками.

Сами “большие” треугольники, с вершинами на вершинах икосаэдра также имеют структуру. На acidome в режиме кровли это видно по цвету. Треугольники расположены симметрично относительно центра “большого” треугольника. Количество их типов меньше общего числа треугольников. В случае с частотой 5 уникальных треугольников 9.

В процессе проектирования дома я столкнулся с задачей постройки сферы в Dynamo. Это такой инструмент, который позволяет научить Autodesk Revit работать со сложными формами. Такая среда визуального программирования.
Погуглив я даже нашел скетч, который в Dynamo строил геодезическую сферу. Сферу то он строил, да не ту.

Дело вот в чем. Когда мы берем одно ребро икосаэдра и делим его на мелкие треугольники — сделать это можно несколькими способами. В acidome за это отвечает переключатель “метод разбиения”.

Найденный скетч строил сферу методом равных хорд. Что это значит? Мы берем большой треугольник икосаэдра, каждое его ребро делим на нужное нам количество частей, соединяем точки на ребрах между собой и получаем плоскую сетку из треугольников. Затем эту сетку мы проецируем на сферу. Все бы хорошо, но сами эти треугольники достаточно сильно отличаются по размеру. Центральный больше всех. Оно и понятно, центр “большого” треугольника у нас на максимальном расстоянии от сферы. Это плохо, так как в этом случае сложнее оптимизировать расход материалов. Будет больше отходов.

Другой метод разбиения (равными дугами) предполагает, что мы строим поверх “большого” треугольника дуги и уже их делим на равные части. Подход отличается, простой проекцией не обойтись.

Скетч не подходил. Я попытался его исправить и в итоге мне пришлось нырнуть в это дело с головой.

Как оказалось помимо визуальной среды Dynamo имеет встроенный Python. С этим языком я ранее не сталкивался, но где наша не пропадала? В конце концов это просто инструмент.

Дальше будут кусочки кода, прошу обратить внимание, что это мой hello world в python, а целью было не построить максимально эффективное и производительное решение, а построить нужную сферу.

Метод равных дуг.

Берем одну из граней икосаэдра и из углов этого треугольника строим дуги.

Затем дуги делим на равные части и соединяем точки на дугах новыми дугами. У всех дуг один центр — центр сферы. Точки соединяем не все со всеми, а одноименные. На картинке оно выглядит попроще, чем в коде.

Опа, а дуги то не пересекаются! Не слишком беглое гугление вывело меня на книгу, которая подтвердила мои предположения о том, что нужно в качестве вершины ребра геодезика использовать центр треугольника, образованного пересечением дуг. Также курил исходники acidome, но не помню нашел ли там этому подтверждение. Помню, что было интересно.
Центры надо как-то найти. Это центр треугольника и это не сложно, но нужно было понять где же у нас в ворохе точек эти треугольники. Мне показалось самым простым вариантом соединять ближайшие друг к другу точки.

Теперь нам нужно соединить между собой собранные на разных этапах точки, которые и являются вершинами ребер геодезической сферы. На картинке эти точки видно хорошо, но вот когда они в массиве — все сложнее. Было несколько вариантов, но так как задача была с наименьшими трудозатратами получить рабочий скрипт, вышло вот это:

Сегмент готов. Наверное существует какой-то правильный путь для решения этой задачи, но я проложил свой.

Дальше сегмент разворачивается, несколько раз копируется копируется и получается полная сфера. Вот один из поворотов:

Скриптик вышел страшненький, я его пару раз переписывал, так как были проблемы с экспортом в Revit. Думал, что проблемы с построением. В итоге на форуме Dynamo индус подсказал украинцу и все удалось!

Теперь можно строить сферу любой частоты и любого диаметра. Сравнение размеров с результатами acidome показало, что все сходится с высокой точностью. Повторяемость это хорошо.

Также я занялся оптимизацией размеров с целью минимизации обрезков. Так как все размеры были у меня на руках это было не так трудно. В итоге радиус сферы получился 5,65 метров при частоте 5. Такие размеры позволяют мне достаточно эффективно использовать материалы шириной 125 см. Такую ширину имеют листы OSB, листового металла, утеплителя, гипсокартона. При хорошей оптимизации количество обрезков минимально. Наилучших результатов можно добиться путем расчета раскладок треугольников на материале, но этим я не занимался.

Дальше было проще, так как Revit съел сложную форму и позволил с ней работать примерно с тем же успехом, что и с квадратно-параллельной.

Конечно, трудности на этом не закончились, но это уже совсем другая история.

Источник

Инструкция к калькулятору для расчёта купольной крыши и купольного дома

Данная страница — инструкция к калькулятору для расчёта купольных конструкций, в том числе купольных крыш и купольных домов.

Страница с калькулятором находится по ссылке: калькулятор.

По умолчанию выставлен русский язык интерфейса. Его можно сменить на удобный для Вас, выбрав нужный в выпадающем списке «Язык».

выбор языка интерфейса

Инструкция к калькулятору

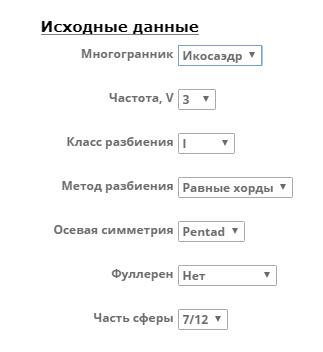
Исходные данные.

Область «Исходные данные» предназначена для задания геометрии каркаса. Можно изменять параметры в следующих полях:

«Многогранник» — многогранник на основание которого строится вся конструкция. Возможны два варианта: икосаэдр и октаэдр.

«Частота, V» — количество разбиений вершин. При увеличении частоты, увеличивается количество вершин и ребер соответственно. Чем больше это значение, тем больше форма каркаса приближается к сфере и тем меньше длина рёбер.

Икосаэдр — многогранник, у которого значение частоты разбиения V равно 1. Октаэдр — многогранник, у которого значение частоты разбиения V равно 1.

Значение частоты разбиения равное единице соответствует конструкции в виде икосаэдра или октаэдра в зависимости от того какой многогранник задан в графе «многогранник». При увеличении частоты происходит разбиение рёбер многогранника на части. Количество рёбер, составляющих разбитое ребро, равно частоте разбиения.

Частота разбиения икосаэдра.

«Класс разбиения» — этот пункт отвечает за выбор способа разбиения, а следовательно и формы конечной конструкции.

При частоте разбиения равной двум и более возможны различные варианты каждого разбиения. Эти варианты делятся на классы. Если спроецировать разбиение на грань икосаэдра, то все возможные классы разбиения икосаэдра можно представить в виде схемы.

Классы разбиения купольных конструкций.

В калькуляторе римскими цифрами обозначены основные классы, всего их три. Арабскими цифрами обозначены вариации основных классов.

Аналогично способы разбиения задаются для октаэдра.

«Метод разбиения» — позволяет сделать выбор между «Равные хорды», «Равные дуги» и «Мексиканец».

«Осевая симметрия» — выбор оси симметрии, которая учитывается при отсечении части купола от сферы и выстраивании купола по вертикали. Возможные варианты:

• Pentad — ось симметрии проходит через вершину, в которой сходится 5 рёбер.
• Cross — ось симметрии проходит через вершину, в которой сходится 6 рёбер.
• Triad — ось симметрии проходит через грань.

«Фулерен» — выбор формы купола в виде фулерена, который вписывается («вписанный») в сферу, или описывает её («описанный»). Поле «Фулерен» не доступно при выборе варианта соединения «Joint».

купол в форме фулерена

«Выравнивание основания» — позволяет выравнивать основание относительно плоскости основания за счет изменения длин рёбер у основания купола. Поле «Выравнивание основания» не доступно при выборе способа соединения «Cone» или выборе формы фулерена.

Функция «выравнивание основания» изменят длину рёбер у основания купола таким образом, что вершины купола на внешней его поверхности располагаются в плоскости основания. Вершины купола на внутренней поверхности купола в общем случае не располагаются в плоскости основания, а строятся по общему принципу — к центру купола от его внешней поверхности.

При включении «выравнивания основания» рёбра своей широкой стороной лежат в плоскости горизонта в случае, когда в поле «часть сферы» выбрано 1/2. В остальных случаях, они не лежат в плоскости горизонта.

«Часть сферы» — выбор части сферы, из которой будет состоять купол. Для куполов разной частоты возможны различные пропорции отсечения.

Размеры и способ соединения

Поле «размеры и способы соединения» позволяет задать размеры сферы и выбрать способ соединения ребер купола. Параметры поля:

«Радиус сферы, м» — задается радиус сферы в метрах.

«Способ соединения» — выбор способа соединения рёбер. Более подробно о способах соединения можно посмотреть в статье: Виды соединения и коннекторы (соединители) для купольных конструкций.

В выпадающем списке можно выбрать следующие варианты соединений:

• «Piped» — способ соединения с использованием коннекторов. При выборе данного способа соединений появляется дополнительное поле, в котором можно задать диаметр трубы, составляющей коннектор.
• «GoodKarma» — безконнекторный способ соединения, при котором каждое ребро составляют два бруса. При выборе данного способа соединения появляется дополнительное поле, в котором можно задать способ соединения рёбер по часовой стрелке или против часовой стрелки.
• «Semikone» — безконнекторный способ соединения, при котором каждое ребро составляют два бруса.
• «Cone» — безконнекторный способ соединения, при котором каждое ребро состоит из одного бруса.
• «Joint» — безконнекторный способ соединения, при котором каждое ребро состоит из одного бруса. При выборе данного способа соединения появляется дополнительное поле, в котором можно задать способ соединения рёбер по часовой стрелке или против часовой стрелки. Способ «Joint» не доступен для купола в форме фулерена.
• «Nose» — безконнекторный способ соединения, при котором каждое ребро состоит из одного бруса. Возможность выбора данного способа соединения предусмотрена только для купола в форме фулерена. Чтобы данный способ соединения появился в списке вариантов соединения, нужно предварительно задать форму купола в виде фулерена в поле «Фулерен» в разделе «Исходные данные». Для этого в поле «Фулерен» нужно выбрать один из вариантов: «Вписанный» или «Описанный». При выборе данного способа соединения появляется дополнительное поле, в котором можно задать способ соединения рёбер по часовой стрелке или против часовой стрелки.

Для всех способов соединения рёбра у основания купола состоят из одного бруса.

Для многогранников в виде октаэдра в текущей версии калькулятора не реализован расчет соединения «Cone». Вместо него калькулятор рассчитывает значения, как для типа соединения «Piped» с нулевым диаметром трубы.

Размеры рёбер

В этом поле задаются ширина и толщина рёбер в миллиметрах.

Схема купола

В правой части калькулятора отображается схема заданного купола. Купол можно вращать мышкой и приближать и отдалять его колесом мыши.

В калькуляторе можно посмотреть: каркас, кровлю, схему и план, нажав соответствующую кнопку. Их также можно вращать, увеличивать и уменьшать.

Схема

Кровля

Схема на вкладке «Кровля» позволяет исключать из расчёта отдельные грани и рёбра конструкции. Для исключения грани, нужно щёлкнуть по ней мышкой. Для исключения ребра нужно исключить примыкающие к нему с обеих сторон грани.

При исключении из расчёта граней и рёбер во вкладке «Кровля» значения в других вкладах и разделах калькулятора пересчитываются автоматически.

Данная функция может быть полезна для анализа возможных проёмов в конструкции, например для дверей и окон. А также для расчёта таких конструкций как беседки, навесы, козырьки и другие.

Во вкладке «План» можно увидеть проекцию нижних рёбер конструкции на плоскость в основании. А также размеры от центра сферы до концов проекций и высоту концов рёбер.

Выделив мышкой отдельные рёбра, можно увидеть аналогичную информацию для любого ребра купола.

Повторный щелчок мыши снимает выделение.

Если во вкладке «Кровля» исключена грань купола, то при переходе на вкладку «План» автоматически подсветятся рёбра этих граней.

Чтобы увидеть план основания полностью, вращайте схему курсором.

Результаты измерений

Содержимое блока «результаты измерений» становится видимым при щелчке по заголовку этого блока «результаты измерений».

Блок с результатами измерений

Название каждого поля отвечает само за себя.

В блоке «Размеры» указано количество размеров и количество самих элементов:

«Граней» — первое число указывает количество размеров, второе число показывает количество граней. На схеме грани одного размера показаны одним цветом.

«Ребер» — первое число указывает количество размеров, второе число показывает количество рёбер. На схеме рёбра одного размера показаны одним цветом и обозначены одинаковыми буквами.

«Вершин» — первое число указывает количество вершин к которым подводятся разные рёбра без учета того, что к вершинам у снования подводится меньше рёбер. Второе число показывает количество вершин.

Рёбра

В блоке рёбра показаны вид, размеры и количество всех рёбер рассчитанного купола.

На схеме используются следующие обозначения:

Обозначения на чертежах рёбер

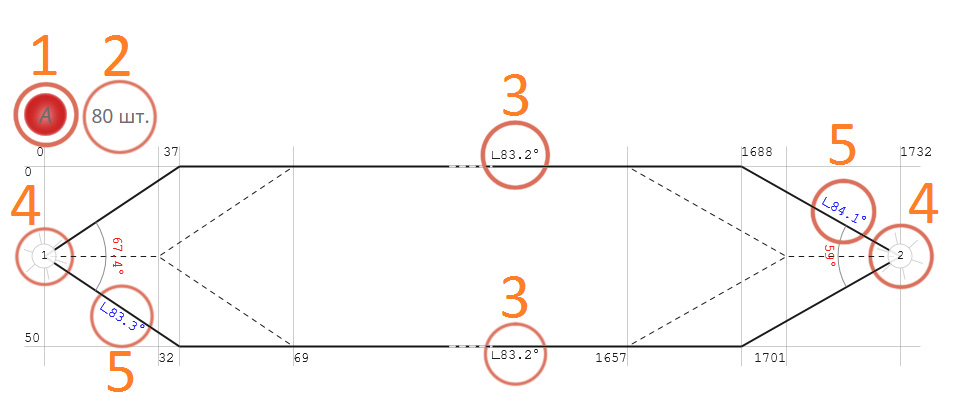
1. Индекс ребра и его цвет на схеме. В качестве индекса используются латинские буквы.
2. Количество рёбер данного типа (индекса).
3. Значение двугранного угла между плоскостью ребра и прилегающей к нему гранью купола.
4. Числовое обозначение вершины, в которую ребро упирается данным концом.
5. Значение двугранного угла между внешней плоскостью ребра и плоскостью отреза.

Если правая сторона рёбер выводится не корректно, то увеличьте ширину окна браузера, в котором открыт калькулятор. Рекомендуемая ширина 1920 пикселей.

При распиле рёбер торцовочной пилой иногда удобно ориентировать ребро широкой стороной вниз. Тогда углы поворота пилы будут отличаться от полученных здесь. Для их пересчёта можно воспользоваться отдельным калькулятором углов торцовочной пилы.

Грани

В блоке грани показаны вид, размеры и количество всех граней рассчитанного купола.

Вершины

В блоке вершины показаны вид, размеры и количество всех вершины рассчитанного купола. Вершины приведены без учета отсечения части сферы от купола. Так если одно или несколько рёбер имеет обозначение «undefined», то это значит что в усеченном куполе такие вершины есть у основания и граней с обозначением «undefined» у них нет. Для того чтобы увидеть все грани, в поле «часть сферы» следует выбрать всю сферу «1/1».

Результаты конструирования

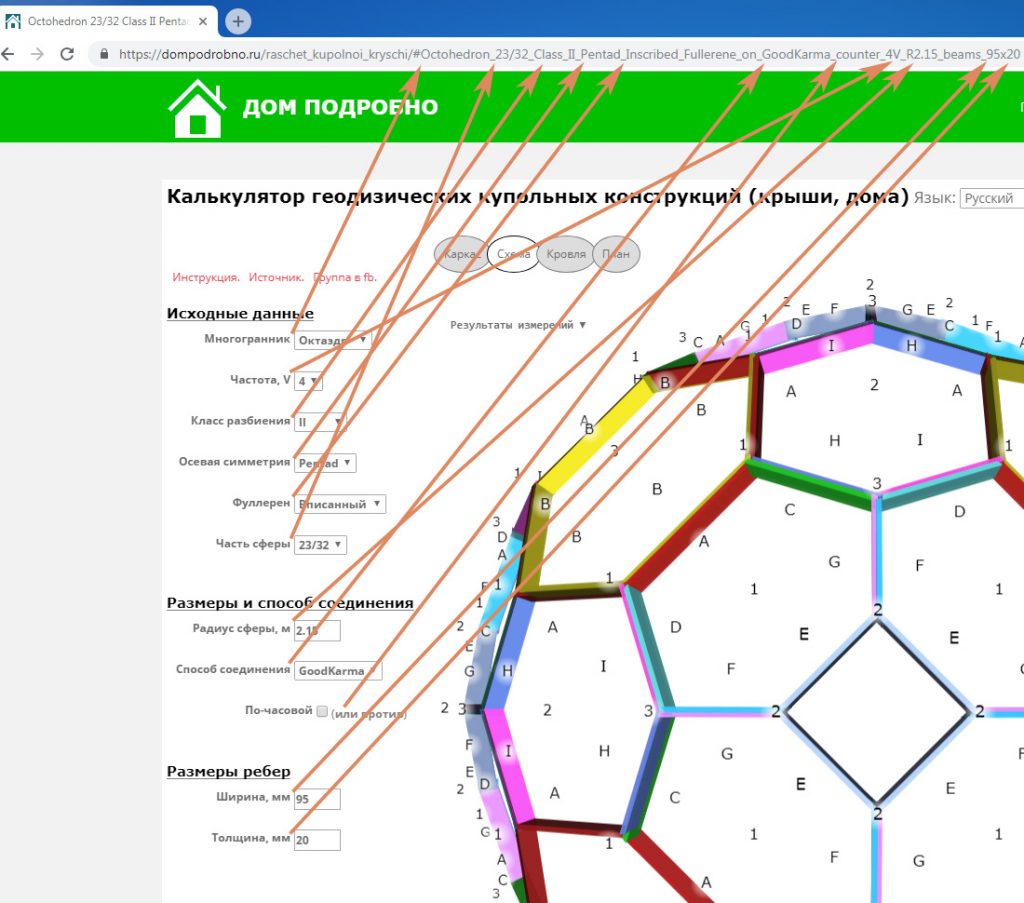
Чтобы сохранить результаты конструирования можно воспользоваться адресом страницы калькулятора, который автоматически меняется в зависимости от введенных данных.

Получившуюся ссылку удобно использовать для передачи другим людям купольной конструкции, с заданными Вами параметрами.

Скачать модель получившейся конструкции в формате .obj можно с помощью кнопки «выгрузить». Она расположена после результатов вычислений в нижней части страницы в блоке полезных ссылок.

Блоки калькулятора

Открывая страницу калькулятора на устройствах с самым популярными размерами экранов, можно увидеть только верхнюю область калькулятора. В ней обычно видны блоки:

• «Исходные данные»
• «Результаты и способы соединения»
• «Размеры ребер»
• «Результаты измерений»
• Схема купола
• Кнопки переключения вкладок: «Каркас», «Схема», «Кровля», «План».

Чтобы увидеть блоки с чертежами рёбер и схемами граней и вершин, нужно прокрутить страницу вниз.

Общий вид страницы калькулятора.

Источник