Решающие деревья и их композиции. Практика.
Здесь я хочу разобрать задания из курса https://www.coursera.org/learn/supervised-learning/. Задания неплохо (на мой взгляд) связывают теорию и практику и показывает основные особенности работы со случайным лесом, что очень полезно для практики. Я сначала разберу задание по случайному лесу а затем по градиентному бустингу.
Случайный лес.
Суть задания очень простая. Нужно взять датасет рукописных чисел и пообучать разные деревья на нем что бы посмотреть, как различные алгоритмы влияют на качество при кросс валидации. Сначала нужно подготовить данные.
Данные состоят из 1797 объектов для каждого из которых заданы 64 признака и соответсвующие метки классов:
Попробуем нарисовать чиселки из датасета.
В задании нужно измерять качество работы классификаторов на кросс валидации c 10 фолдами, поэтому сразу напишем функцию для общего интерфейса и заодно функцию для рисования тех чисел, где классификатор ошибся.
Хорошо, теперь можно приступать к обучению. Сначала начинам с дерева решения.
Создайте DecisionTreeClassifier с настройками по умолчанию и измерьте качество его работы с помощью cross_val_score.
Так и сделаем, только зафиксируем random_state чтобы результаты были воспроизводимы и заодно посмотрим на каких числах классификатор ошибался.
Получили примерно 82 процента точности что в принципе неплохо и по некоторым картинкам не совсем понятно какое число изображено. Идем дальше.
Воспользуйтесь BaggingClassifier из sklearn.ensemble, чтобы обучить бэггинг над DecisionTreeClassifier. Используйте в BaggingClassifier параметры по умолчанию, задав только количество деревьев равным 100.
У нас уже есть решающее дерево и нам нужно обучить беггинг над ним. Вспомним, что беггинг это среднее значение всех алгоритмов на бутстрепе подвыборок. Значит нам нужно создать класс BaggingClassifier и передать ему в параметры дерево решений. Так и сделаем
Видим, что качество сильно возросло. Но как мы помним, такая композиция все же немного коррелирована, так как все деревья обучаются на одних и тех же признаках. И тут есть два варианта.
Теперь изучите параметры BaggingClassifier и выберите их такими, чтобы каждый базовый алгоритм обучался не на всех d признаках, а на $\sqrt
$ случайных признаков.
Сейчас нужно выбрать $\sqrt
Качество чуть выросло, но тут мы использовали рандомную выборку из $\sqrt
Наконец, давайте попробуем выбирать случайные признаки не один раз на все дерево, а при построении каждой вершины дерева. Сделать это несложно: нужно убрать выбор случайного подмножества признаков в BaggingClassifier и добавить его в DecisionTreeClassifier.
Пока что получили самую большую точность — 95% процентов по кросс валидации. Последний построенный классификатор напоминает случайный лес, так как мы делаем беггинг и случайный отбор признаков и поэтому мы можем сравнить наш классификатор со случайным лесом, что и предлагается в следующем задании.
Полученный в пункте 4 классификатор — бэггинг на рандомизированных деревьях (в которых при построении каждой вершины выбирается случайное подмножество признаков и разбиение ищется только по ним). Это в точности соответствует алгоритму Random Forest, поэтому почему бы не сравнить качество работы классификатора с RandomForestClassifier из sklearn.ensemble. Сделайте это, а затем изучите, как качество классификации на данном датасете зависит от количества деревьев, количества признаков, выбираемых при построении каждой вершины дерева, а также ограничений на глубину дерева. Для наглядности лучше построить графики зависимости качества от значений параметров
Давайте сначала оценим работу RF от количества деревьев.
Интересные получились результаты. Во первых, так как мы не ограничивали деревья в глубину, то алгоритм долго работал на тестовом датасете. Во вторых, средняя точность при разном кол-ве деревьев такая же, как и в случае беггинга на рандомных признаках, что и показывает применение всей вышеизложенной теории. А что касается зависимости точности от кол-ва деревьев, то судя по графику можно смело сказать, что алгоритм выходит на константу и дальнейшее увеличение деревьев не влияет на результат (вообще у меня сильно зависит от random_state). Посмотрим теперь как зависит качество от кол-ва рандомных признаков.
Интересно, что предположение о том, что нужно брать где то $\sqrt
Из графика видно, что чем больше глубина, тем больше точность предсказания. Но у нас время обучения значительно упало.
Итак, теперь можно ответить на вопросы в задании:
1) Случайный лес сильно переобучается с ростом количества деревьев
Нет, это не так. Каждое дерево в случайном лесе сильно переобучается, а качество обучения композиции деревьев выходит на некую константу в зависимости от числа деревьев в композиции.
2) При очень маленьком числе деревьев (5, 10, 15), случайный лес работает хуже, чем при большем числе деревьев
Да, это так. При композиции алгоритмов разброс ошибки обратно пропорционален кол-ву алгоритмов, поэтому при маленьком числе деревьев качество хуже, чем при большом. Это и показано на графике выше.
3) С ростом количества деревьев в случайном лесе, в какой-то момент деревьев становится достаточно для высокого качества классификации, а затем качество существенно не меняется.
Да, это в точности отражено на графике.
4) При большом количестве признаков (для данного датасета — 40, 50) качество классификации становится хуже, чем при малом количестве признаков (5, 10). Это связано с тем, что чем меньше признаков выбирается в каждом узле, тем более различными получаются деревья (ведь деревья сильно неустойчивы к изменениям в обучающей выборке), и тем лучше работает их композиция.
Все абсолютно верно. Чем меньше признаков, тем менее коррелированы становятся деревья. Но надо понимать, что слишком малое кол-во признаков не позволит “поймать” зависимость в данных.
5) При большом количестве признаков (40, 50, 60) качество классификации лучше, чем при малом количестве признаков (5, 10). Это связано с тем, что чем больше признаков — тем больше информации об объектах, а значит алгоритм может делать прогнозы более точно.
Нет, это не верно. Почему это неверно, написано выше.
6) При небольшой максимальной глубине деревьев (5-6) качество работы случайного леса намного лучше, чем без ограничения глубины, т.к. деревья получаются не переобученными. С ростом глубины деревьев качество ухудшается.
Нет, это не так. Чем более переобучено дерево тем лучше это для композиции. Переобучение нам здесь на руку.
7) При небольшой максимальной глубине деревьев (5-6) качество работы случайного леса заметно хуже, чем без ограничений, т.к. деревья получаются недообученными. С ростом глубины качество сначала улучшается, а затем не меняется существенно, т.к. из-за усреднения прогнозов и различий деревьев их переобученность в бэггинге не сказывается на итоговом качестве (все деревья преобучены по-разному, и при усреднении они компенсируют переобученность друг-друга).
Да, это так, что и подтверждают графики выше.
Таким образом решающие деревья и их композиции очень крутой и простой инструмент машинного обучения. Случайный лес работает из коробки и позволяет достичь очень большой точности даже на стандартных параметрах.
Градиентный бустинг
В этом задании нужно будет реализовать градиентный бустинг над деревьями своими руками, благо сделать это не сложно. Мы будем работать с другим датасетом boston для задачи регресии (видимо, потому что производную считать просто). Загрузим датасет и подготовим данные
Всего у нас 506 объектов. Мы 25% выборки откладываем на тест. Отлично, теперь можно приступать к заданию. Нужно построить градиентный бустинг для 50 деревьев DecisionTreeRegressor(max_depth=5, random_state=42) на датасете. Из теории мы помним, что каждое новое дерево обучается на антиградиенте ошибки композии по прошлым деревьям. Ошибка в этом случае считается как квадрат отклонения предсказания композиции от истинного ответа. Значит, что бы обучать каждое новое дерево нужно считать градиент квадратичной функции потерь. Далее, после обучения нового дерева его нужно с неким коэффициентом добавить в композицию. После 50 итераций это и будет наш бустинг.
Итак, начнем с производной. Нам нудно найти такой вектор $\bar<\xi>$, чтобы он минимизировал среднеквадратичную ошибку:
\[\sum_
Этот вектор будет равен вектору антиградиента, где каждая компонента это частная производная по $\xi_i$ (знак + потому что антиградиент уже учтен):
Теперь вектор антиградиента мы знаем, поэтому можно начать обучать алгоритмы на этот вектор. Предлагается использовать следующую функцию для удобства
Для каждого элемента в выборке $X$ считается сумма предсказаний алгоритма algo из массива алгоритмов base_algorithms_list вместе коэффициентами из массива coefficients_list. Что бы нам посчитать градиенты, нам нужны ответы и предсказания композиции для прошлого шага. Так и запишем (двойка в производной опущена по рекомендации):
Эта функция будет возвращать пересчитанный антиградиент композиции. Теперь нужно обучить 50 деревьев на этих градиентах:
Видно, что средняя квадратичная ошибка по отложенной выборке составляет 5.55. Далее предлагают посмотреть, что если коэффициенты будет зависеть от номера итерации?
На самом деле у меня ошибка не сильно упала. Давайте посмотрим, как справится с этой задачей нормальный градиентный бустинг.
Видно, что ошибка не сильно отличается. Давайте понаблюдаем, как результат будет зависеть от числа деревьев и глубины?
Из графиков видно, что алгоритм сильно переобучается с ростом глубины дерева. Примерно тоже самое наблюдается для числа деревьев. Т.е. рекомендации простые — аккуратно увеличивать число деревьев и их глубину пока это будет снижать ошибку. Ну и напоследок предлагается сравнить результат с линейной регрессией, но я пропущу этот шаг. Понятно, что простая модель не может восстановить сложную зависимость в данных.
Источник
Градиентый бустинг — просто о сложном
Хотя большинство победителей соревнований на Kaggle используют композицию разных моделей, одна из них заслуживает особого внимания, так как является почти обязательной частью. Речь, конечно, про Градиентный бустинг (GBM) и его вариации. Возьмем, например. победителя Safe Driver Prediction, Michael Jahrer. Его решение — это комбинация шести моделей. Одна LightGBM (вариация GBM) и пять нейронных сетей. Хотя его успех в большей мере принадлежит полуконтролируемому обучению, которое он использовал для упорядочивания данных, градиентный бустинг сыграл свою роль.
Даже несмотря на то, что градиентный бустинг используется повсеместно, многие практики до сих пор относятся к нему, как к сложному алгоритму в черном ящике и просто запускают готовые модели из предустановленных библиотек. Цель этой статьи — дать понимание как же работает градиентный бустинг. Разбор будет посвящен чистому “vanilla” GMB.
Ансамбли, бэггинг и бустинг
Когда мы пытаемся предсказать целевую переменную с помощью любого алгоритма машинного обучения, главные причины отличий реальной и предсказанной переменной — это noise, variance и bias. Ансамбль помогает уменьшить эти факторы (за исключением noise — это неуменьшаемая величина).
Ансамбль
Ансамбль — это набор предсказателей, которые вместе дают ответ (например, среднее по всем). Причина почему мы используем ансамбли — несколько предсказателей, которые пытаюсь получить одну и ту же переменную дадут более точный результат, нежели одиночный предсказатель. Техники ансамблирования впоследствии классифицируются в Бэггинг и Бустинг.
Бэггинг
Бэггинг — простая техника, в которой мы строим независимые модели и комбинируем их, используя некоторую модель усреднения (например, взвешенное среднее, голосование большинства или нормальное среднее).
Обычно берут случайную подвыборку данных для каждой модели, так все модели немного отличаются друг от друга. Выборка строится по модели выбора с возвращением. Из-за того что данная техника использует множество некореллириющих моделей для построения итоговой модели, это уменьшает variance. Примером бэггинга служит модель случайного леса (Random Forest, RF)
Бустинг
Бустинг — это техника построения ансамблей, в которой предсказатели построены не независимо, а последовательно
Это техника использует идею о том, что следующая модель будет учится на ошибках предыдущей. Они имеют неравную вероятность появления в последующих моделях, и чаще появятся те, что дают наибольшую ошибку. Предсказатели могут быть выбраны из широкого ассортимента моделей, например, деревья решений, регрессия, классификаторы и т.д. Из-за того, что предсказатели обучаются на ошибках, совершенных предыдущими, требуется меньше времени для того, чтобы добраться до реального ответа. Но мы должны выбирать критерий остановки с осторожностью, иначе это может привести к переобучению. Градиентный бустинг — это пример бустинга.
Алгоритм градиентного бустинга
Градиентный бустинг — это техника машинного обучения для задач классификации и регрессии, которая строит модель предсказания в форме ансамбля слабых предсказывающих моделей, обычно деревьев решений.
Цель любого алгоритма обучения с учителем — определить функцию потерь и минимизировать её. Давайте обратимся к математике градиентного бустинга. Пусть, например, в качестве функции потерь будет среднеквадратичная ошибка (MSE):
Мы хотим, чтобы построить наши предсказания таким образом, чтобы MSE была минимальна. Используя градиентный спуск и обновляя предсказания, основанные на скорости обучения (learning rate), ищем значения, на которых MSE минимальна.
Итак, мы просто обновляем предсказания таким образом, что сумма наших отклонений стремилась к нулю и предсказанные значения были близки к реальным.
Интуиция за градиентным бустингом
Логика, что стоит за градиентым бустингом, проста, ее можно понять интуитивно, без математического формализма. Предполагается, что читатель знаком с простой линейной регрессией.
Первое предположение линейной регресии, что сумма отклонений = 0, т.е. отклонения должны быть случайно распределены в окрестности нуля.
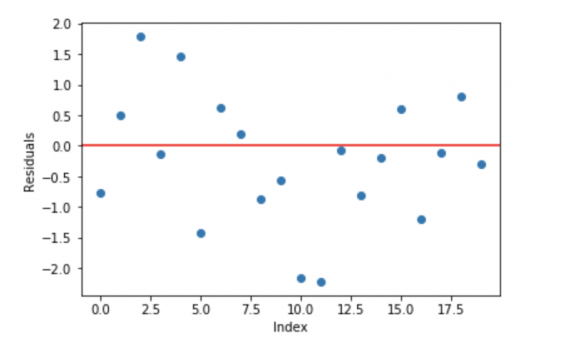
Теперь давайте думать о отклонениях, как об ошибках, сделанных нашей моделью. Хотя в моделях основанных на деревьях не делается такого предположения, если мы будем размышлять об этом предположении логически (не статистически), мы можем понять, что увидив принцип распределения отклонений, сможем использовать данный паттерн для модели.
Итак, интуиция за алгоритмом градиентного бустинга — итеративно применять паттерны отклонений и улучшать предсказания. Как только мы достигли момента, когда отклонения не имеют никакого паттерна, мы прекращаем достраивать нашу модель (иначе это может привести к переобучению). Алгоритмически, мы минимизируем нашу функцию потерь.
- Сначала строим простые модели и анализируем ошибки;
- Определяем точки, которые не вписываются в простую модель;
- Добавляем модели, которые обрабатывают сложные случаи, которые были выявлены на начальной модели;
- Собираем все построенные модели, определяя вес каждого предсказателя.
Шаги построения модели градиентного спуска
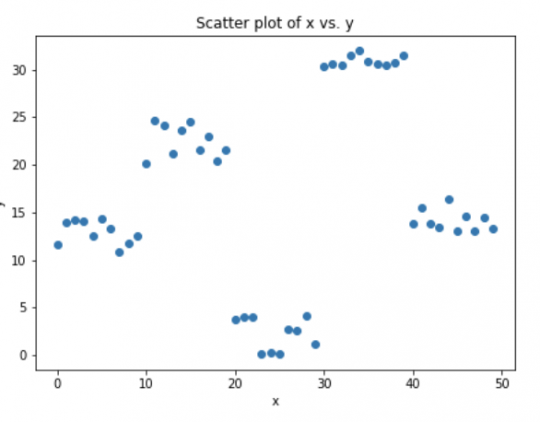
Рассмотрим смоделированные данные, как показано на диаграмме рассеивания ниже с 1 входным (x) и 1 выходной (y) переменными.
Данные для показанного выше графика генерируются с использованием кода python:
1. Установите линейную регрессию или дерево решений на данные (здесь выбрано дерево решений в коде) [вызов x как input и y в качестве output]
2. Вычислите погрешности ошибок. Фактическое целевое значение, минус прогнозируемое целевое значение [e1 = y — y_predicted1]
3. Установите новую модель для отклонений в качестве целевой переменной с одинаковыми входными переменными [назовите ее e1_predicted]
4. Добавьте предсказанные отклонения к предыдущим прогнозам
[y_predicted2 = y_predicted1 + e1_predicted]
5. Установите еще одну модель оставшихся отклонений. т.е. [e2 = y — y_predicted2], и повторите шаги с 2 по 5, пока они не начнутся overfitting, или сумма не станет постоянной. Управление overfitting-ом может контролироваться путем постоянной проверки точности на данных для валидации.
Чтобы помочь понять базовые концепции, вот ссылка с полной реализацией простой модели градиентного бустинга с нуля.
Приведенный код — это неоптимизированная vanilla реализация повышения градиента. Большинство моделей повышения градиента, доступных в библиотеках, хорошо оптимизированы и имеют множество гиперпараметров.
Визуализация работы Gradient Boosting Tree:
- Синие точки (слева) отображаются как вход (x) по сравнению с выходом (y);
- Красная линия (слева) показывает значения, предсказанные деревом решений;
- Зеленые точки (справа) показывают остатки по сравнению с вводом (x) для i-й итерации;
- Итерация представляет собой последовательное заполнения дерева Gradient Boosting.
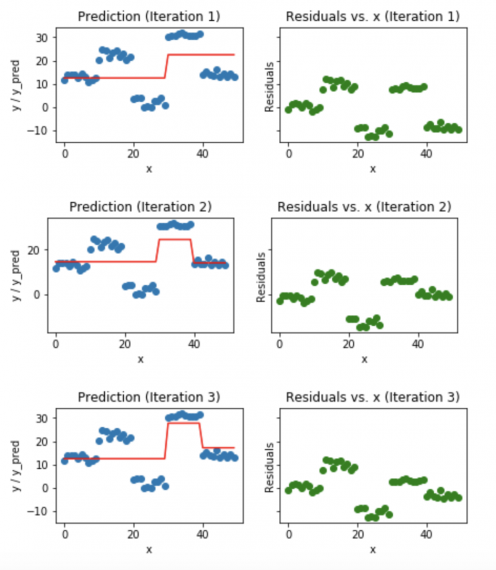
Заметим, что после 20-й итерации отклонения распределены случайным образом (здесь не говорим о случайной норме) около 0, и наши прогнозы очень близки к истинным значениям (итерации называются n_estimators в реализации sklearn). Возможно, это хороший момент для остановки, или наша модель начнет переобучаться.
Посмотрим, как выглядит наша модель после 50-й итерации.
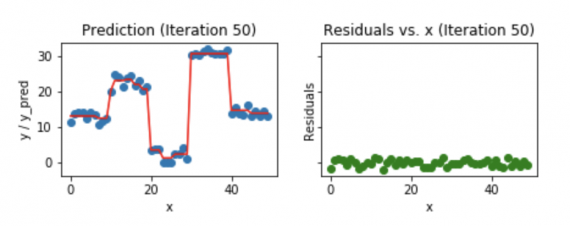
Мы видим, что даже после 50-й итерации отклонения по сравнению с графиком x похожи на то, что мы видим на 20-й итерации. Но модель становится все более сложной, и предсказания перерабатывают данные обучения и пытаются изучить каждый учебный материал. Таким образом, было бы лучше остановиться на 20-й итерации.
Фрагмент кода Python, используемый для построения всех вышеперечисленных графиков.
Видео Александра Ихлера:
Источник