Мастер-класс по изготовлению дидактической игры для детей старшего дошкольного возраста «Судоку»
Елена Чувилина
Мастер-класс по изготовлению дидактической игры для детей старшего дошкольного возраста «Судоку»
Дидактическая игра для детей старшего возраста «Судоку»
Цель игры: развитие наблюдательности, внимания, памяти, логического мышления; закрепление знания цветов; закрепление знания геометрических фигур, цифр, знаков; ориентировка на микроплоскости.
Правила: На игровом поле из 9 (16) клеток необходимо разместить геометрические фигуры так, чтобы в каждом столбике и строке каждая фигура встречалась только один раз. Для начала нужно рассмотреть карточку с заданием, затем найти ряды, в которых уже по условию известны фигуры. Найти необходимые среди разрезных и положить на пустую клетку игрового поля. Проверить и потом двигаться дальше. И так до тех пор, пока не заполнятся все пустые клетки на карточке.
Усложнённый вариант: У детей только пустое игровое поле. Нужно разложить квадратики по своим местам, опираясь на ранее полученные знания.
Для изготовления игры нам потребуется: цветной и белый картон, самоклеющаяся бумага, блокнот, ножницы, карандаш, черный фломастер, офицерская линейка.
1. Для образца в блокноте на страницах расчерчиваем фломастером поля, сначала на 9 ,затем на 16 частей.
2. На белом картоне расчерчиваем такие же поля, как и в блокноте, для выкладывания на них геометрических фигур по образцу.
3. По шаблону вырезаем геометрические фигуры из самоклеющейся бумаги и наклеиваем на поля в блокноте.
4. Распечатываем на принтере название игры, ее цель и правила, наклеиваем на белый картон и на титульный лист блокнота; а также надписи для выполнения задания и наклеиваем их на страницах блокнота.
Спасибо за внимание!
«Грибок-теремок». Мастер-класс по изготовлению пособия для дидактической игры Доброе время суток друзья, коллеги и гости моего блога! Сегодня хочу представить Вашему вниманию мастер-класс по изготовлению пособия.
Конспект НОД по ФЭМП для детей старшего дошкольного возраста с использованием дидактической игры «Рыбалка» НОД по ФЭМП для детей старшего дошкольного возраста с использованием дидактической игры «Рыбалка» Программное содержание: Образовательная.
Конспект проведения дидактической игры по развитию произвольной памяти детей старшего дошкольного возраста «Продолжи ряд» Цель: развитие произвольного запоминания. Оборудование: муляжи овощей и фруктов, кукла, 2 корзинки — одна с крышкой. Ход игры: Игра проводится.
Мастер-класс «Игры и эксперименты как средство экологического воспитания детей старшего дошкольного возраста» Муниципальное Общеобразовательное Учреждение «Ыныргинская средняя общеобразовательная школа» Детский сад «Солнышко» «Игры и эксперименты,.
Мастер-класс по изготовлению дидактической игры «Четвертый лишний. Геометрические фигуры» Хочу представить Вашему вниманию дидактическую игру «Четвертый лишний» на обобщение и закрепление знаний о геометрических фигурах и цвете.
Мастер-класс по изготовлению дидактической игры «Дерево» Когда познакомилась с блоками Дьенеша, то просто влюбилась в них. Игру «Дерево помню еще со времен учебы в пед училище, но мы ее на ватмане.
Мастер-класс по изготовлению дидактической игры для детей раннего возраста «Яблоня и 4 Времени года» Мастер — класс по изготовлению дидактической игры для детей раннего возраста «ЯБЛОНЯ И 4 ВРЕМЕНИ ГОДА» Автор — Карепова Людмила Юрьевна.
Мастер-класс по изготовлению дидактической игры «Кто что ест» Для работы нам понадобятся: коробочка (лучше 8-и угольная, но подойдёт и круглая, я нашла коробочку из-под конфет «Мерлетто») а также.
Мастер-класс по изготовлению дидактической игры «Слонёнок» Добрый вечер уважаемые коллеги! хочу представить вашему вниманию «Дидактического слонёнка» Моим малышам слонёнок пришёлся по душе,дети с.
«Пушистая графика». Мастер-класс по изготовлению поделок из тополиного пуха для старшего дошкольного возраста ЗАГОТОВКА ИЗ ТОПОЛИНОГО ПУХА Сбор тополиного пуха рекомендуется проводить в начале июня. Когда в серёжках тополя созревают коробочки,.
Источник
Судоку своими руками
Хочу рассказать вам, дорогие читатели блога, об одной своей программке на Icon, о которой очень хотелось рассказать когда-то давно (еще в 2016 году), но тогда не хватало времени, чтобы описать свой игровой эксперимент. Так уж сложилось, что самое интересное, что я делаю на Icon — это игры, и данный случай — не исключение.
Дело в том, что у меня папа очень любит одну японскую головоломку, а мне явно не хватало вдохновения и идеи, чего бы такого запрограммировать, поэтому после недолгих размышлений, я решил для папы написать свою реализацию судоку, а что из этого получилось, вы можете увидеть заглянув под кат этой статьи.
Итак, начнем с того, что такое судоку.
Судоку — это популярная японская головоломка, которая представляет собой цифровое поле 9 на 9 клеток, в котором уже поставлены некоторые цифры от 1 до 9. Также, внутри квадрата 9 на 9, есть разделение линиями на меньшие квадраты размером 3 на 3. Это разделение существует с одной стороны для облегчения решения головоломки, с другой стороны, оно является непосредственным элементом самих правил.
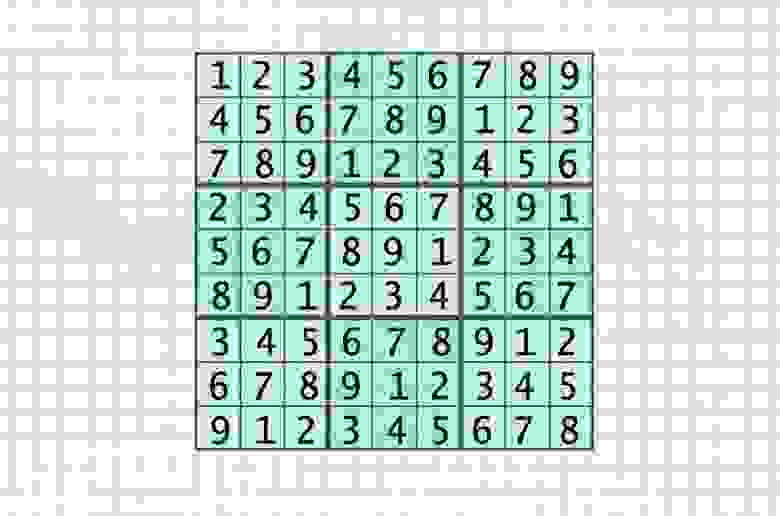
Вот так выглядит обычное поле для игры в судоку:
Правила судоку интуитивно просты и понятны: нужно заполнить все игровое поле цифрами от 1 до 9 таким образом, чтобы цифры в строке или столбце не повторялись, при этом также важен тот факт, что в квадратах 3 на 3, также не должно быть повторяющихся цифр. Поскольку, на поле уже присутствуют некоторые из цифр, то располагая этой информацией и необходимо поставить недостающие (согласно описанным правилам), и таким образом осуществить решение самой головоломки.
Теперь можно приступить к реализации задуманного…
Для построения судоку нам необходимо создать саму сетку и разместить в ней некоторым образом цифры, сгенерировав их абсолютно случайным образом:
Работают эти процедуры так: сначала с помощью процедуры grid, мы в окне программы просто чертим серую сетку из 81 квадрата (т.е. делаем обычное игровое поле, размером 9 на 9); затем с помощью процедуры square мы выделяем жирными черными линиями 9 квадратов размером 3 на 3 (т.е. разделяем игровое поле на несколько крупных квадратов, согласно правилам судоку); далее используя вспомогательную процедуру lremove для удаления из списка n-ого элемента реализуем необходимую нам далее процедуру r_str, которая формирует одну строку нашего судоку и которая пригодиться нам далее.
Теперь, начинается самое интересное: создание алгоритма построения судоку из одной строки случайно сгенерированных неповторяющихся цифр (вот зачем нам процедура r_str).
Алгоритм построения судоку после очень долгих раздумий получился таким: сначала мы берем строку случайных цифр, а затем создаем из нее 8 оставшихся строк с помощью сдвига самой строки на некоторые фиксированные значения сдвига вправо (данные значения были найдены в ходе долгих поисков по интернету и некоторых экспериментов), затем все 9 строк из цифр мы размещаем на игровом поле, после чего случайным образом стираем некоторое количество цифр (количество цифр определено экспериментально).
Реализация соответственно будет такой:
Также нам потребуется создание списка, который будет хранить решение головоломки, поэтому создаем глобальную переменную с пустым списком solv и создаем процедуру рисования всех 9 строк пока без удаления из них цифр:
Процедура удаления цифр также весьма проста:
Поскольку, пока существует сама судоку без стираний, легко определить процедуру отображения решения самой головоломки, сделав его отображение на основе существующих процедур, но в отдельном окне:
Если вспомнить наши предыдущие статьи по созданию всяких мелких игрушек на Icon, то процедуры осуществления хода и его отмены выглядят весьма банально, а изменяется только привязка к конкретным координатам в окне:
Объединим теперь все это в одну программу, собрав все процедуры и импорты в основную процедуру:
Итак, пользователь делает ход, щелкнув левой клавишей мыши по интересующей его клетке и осуществив вод нужной цифры, отмена хода осуществляется щелчком правой клавишей мыши по неправильно поставленной цифре (защита от дурака, к сожалению, не предусмотрена, поскольку писалось все, как говорится, на коленке); а отображение правильного решения осуществляется по нажатию клавиши s.
Это выглядит так:
Подводя итоги, скажу, что мой папа очень был доволен тем, что получил в свои руки классную минималистическую игрушку, за которой он может отдохнуть от работы, однако, для себя я вынес следующую мораль: не стоит писать код в таком стиле, даже если программа делается за один вечер, а необходимо детально вникнуть в проблему и создать качественный код, поскольку внезапно может выясниться, что исходник программы всплывает через несколько лет…
Источник
Алгоритм генерации судоку
Доброго времени суток!
Думаю, головоломка Судоку не нуждается в представлении. Многие из нас проводят за её решением достаточно много времени. Например, когда нужно убить время в дороге или просто поворочать мозги, чтобы не сохли. На хабре есть довольно много постов о решении головоломки. Но когда человек решает с десяток, а может и сотню головоломок, то найдётся пытливый ум, который задаст себе вопрос «А как же получается таблица Судоку, имеющая единственное решение? И как можно описать алгоритм для сетки 9×9?».
Приведённый алгоритм является вполне логичным. Но моей задачей было описание и реализация. Обо всём этом написано под катом.
- Цифра может появиться только один раз в каждой строчке
- Цифра может появиться только один раз в каждом столбике
- Цифра может появиться только один раз в каждом районе (Район — меньший квадрат со стороной 3х3, на изображении ниже выделен фиолетовым цветом)
Шаг 1. Взять за основу базовую сетку
Сетка должна подчинятся правилам Судоку. Размещаем в первую строку 1 2… 8 9, в строках ниже смещаем на 3 позиции влево, т.е. 4 5… 2 3 и 7 8… 5 6.
Далее переходя в следующий район по вертикали смещаем на 1 позицию влево предыдущий район.
В итоге должна получиться вот такая сетка, её я и назову базовой: 
Для реализации создадим класс grid. Заполним его в соответствии с Шагом 1, в котором table — список значений таблицы, метод show — просто наглядный вывод таблицы.
Шаг 2. Перетасовать сетку
Есть несколько видов перестановок, выполнив которые таблица Судоку останется в допустимом состоянии.
К ним относятся:
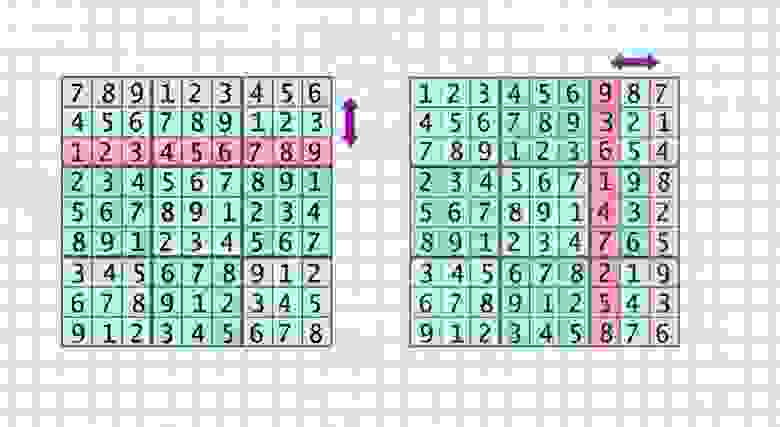
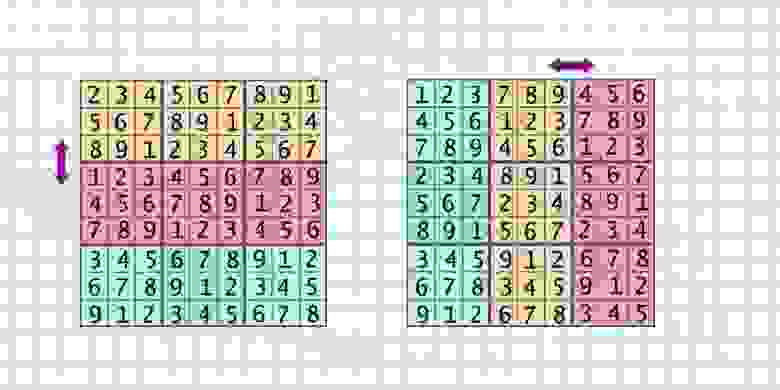
- Транспонирование всей таблицы — столбцы становятся строками и наоборот (transposing)
- Обмен двух строк в пределах одного района (swap_rows_small)
- Обмен двух столбцов в пределах одного района (swap_colums_small)
- Обмен двух районов по горизонтали (swap_rows_area)
- Обмен двух районов по вертикали (swap_colums_area)
Для каждой из перестановок напишем метод:
transposing
swap_rows_small
swap_colums_small
Для обмена столбцов можно поменять строки у транспонированной таблицы:
swap_rows_area
swap_colums_area
Может быть есть ещё более сложные преобразования, но, думаю, можно ограничиться этими. Этот каркас инвариантен своей структуре, такие перестановки есть почти тоже самое, что и действия над матрицами относительно определителя или вращение Кубика Рубика.
Теперь, для того чтобы получить случайную комбинацию, достаточно запустить в случайном порядке функции перемешивания. Так и поступим, amt — количество перемешиваний:
Шаг 3. Удаление клеток
После полученного решения нам необходимо получить задачу (именно в такой последовательности мы можем гарантировать однозначность решения). И это самая сложная часть. Какое количество можно убрать, чтобы гарантировать однозначность решения? Это один из важных факторов, от которого зависит сложность Судоку. Всего в Судоку 81 клетка, обычно считают лёгким когда на поле есть 30-35 «подсказок», средним — 25-30, и сложным — 20-25. Это данные большого набора реальных примеров. Нет никаких законов для сложности. Можно сделать 30-клеточный неразрешимый вариант и 22 клеточный «лёгкий».
- Случайный подход — можно попробовать выкинуть 50-60 клеток наугад, но где вероятность что Судоку можно будет решить? Например, если заполнены 3 строки ( = 27 клеток)
- Случайно с простым ограничением — для примера можно взять некое число N в качестве предела, так что N строк и столбцов могут быть пустыми. Принимая N = 0 — для лёгких уровней, N=1 — средний, N=2 — сложный
Итак, приступим к вычёркиванию ячеек (все варианты равнозначны, поэтому у нас 81 ячейка, которую можно вычеркнуть, поэтому проверим все перебором):
- Выбрать случайную ячейку N
- Отметить N просмотренной
- Удалить N
- Посчитать решения. Если оно не единственное, то вернуть N обратно
На выходе получится самая сложная из возможных вариантов Судоку для данного перемешивания. Переменная difficult оценивает сложность — количество оставшихся элементов.
Я уверен, что есть и более сложные подходы в построении таблицы Судоку. Моя цель была достигнута, получился рабочий алгоритм. Теперь мне не нужно искать новые выпуски, я могу их генерировать 🙂
В принципе, здесь был приведён частный случай Судоку 9х9. Но нет ограничений для использования его на 16х16 и 25х25.
Источник