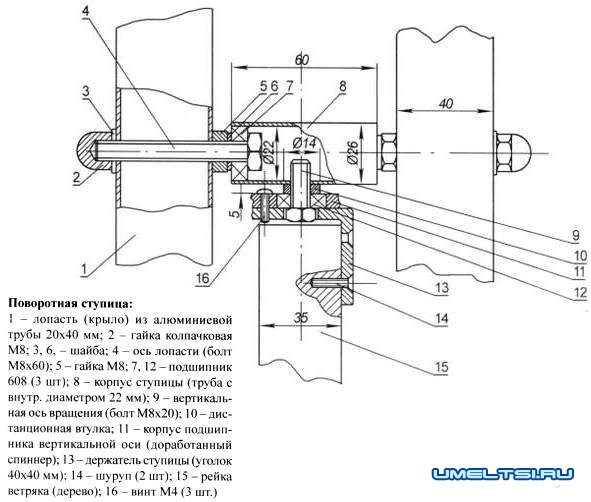
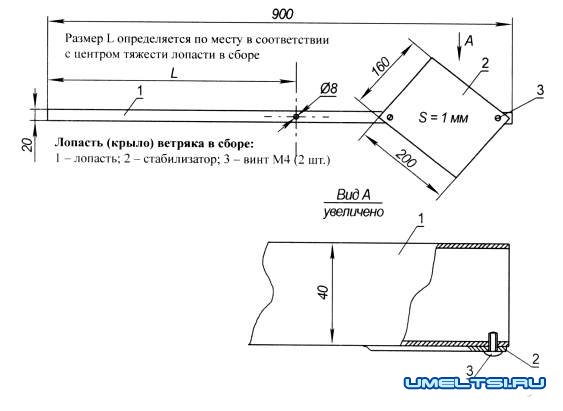
Делаем кинетическую скульптуру своими руками
Сразу скажу, что этот футуристический ветряк придумал не я. Автор этой кинетической скульптуры (то есть не статичной, всем привычной, а подвижной) немецкий художник Майкл Хисчер. «Движущиеся элементы централизованно прикреплены к осям работы и настолько точно уравновешены, что даже малейший ветерок будет приводить их в движение. Мягко сбалансированные крылья каждой скульптуры. находят свой центр в невесомости.
Кинетическая скульптура четырехмерна — когда ее крылья беспорядочно и непредсказуемо скользят по воздуху, они имеют дело с прохождением времени. Легкость и равновесие — их тема, время — их сущность». Так написано на табличке рядом с конструкцией, которую я впервые увидел в московском парке «Зарядье». Есть что-то таинственное в этих лопастях, то поворачивающихся, то замирающих, словно «задумывающихся» о чем-то. Творение Хисчера произвело на меня впечатление даже большее, чем знаменитый парящий мост над Москвойрекой, и я задумал соорудить что-то похожее у себя на дачном участке. Вот народ-то будет дивиться!
Вся соль этой конструкции в очень легком вращении лопастей в вертикальных плоскостях и их ступицы в горизонтальной. Тут нужны хорошие подшипники. Конечно, их можно было бы купить, затем выточить под них ступицу — получилось бы качественно и технически безупречно. Но я не токарь, знакомых, кому можно было бы заказать такую работу, нет, поэтому решил поискать какой-нибудь обходной вариант
Сначала озадачился поиском подходящих подшипников. Приятель, с которым я поделился своей сумасбродной идеей, посоветовал взять их из спиннеров.
Помните, были одно время популярны такие игрушки — их крутили между пальцами и дети, и взрослые. Действительно, вращение у них очень легкое — то, что надо для задуманной конструкции. Но оказалось, что повальное увлечение (а скорее, какой-то массовый психоз) прошло, и спиннеры напрочь исчезли из продажи. В интернет-магазинах они еще встречаются, конечно, но мудрить с оформлением заказа и доставкой попросту не хотелось. Буквально чудом в захудаленьком газетном ларьке нашелся один спиннер — самый простейший, за 20 рублей. Похоже, он валялся на прилавке (или под ним) так долго, что подшипник уже успел немного заржаветь.
Однако сохранил свое легчайшее вращение. Жаль, что в наличии была только одна такая безделушка. Изучение показало, что в ней использован подшипник 608. Диаметр вала 8 мм мне показался вполне подходящим для будущей конструкции. Еще пара подшипников того же типоразмера удачно обнаружились в гараже. А сами лопасти, или крылья, как их именуют в оригинале, решил сделать из прямоугольной дюралюминиевой трубы сечением 20×40 мм, приобретенной на строительном рынке.
Самое сложное — сделать ступицу для лопастей, она же обойма для подшипников. В результате довольно долгих блужданий по свалкам различного металлолома подобрал там кусок стальной трубы с внутренним диаметром ровно 22 мм, что и требовалось. Правда, труба была со швом, чуть выступающим внутрь и мешающим посадке подшипника. Пришлось вооружиться круглым напильником и устранить эту неровность.
Пластмассовый спиннер — это уже своего рода обойма под подшипник, и я решил использовать его под установку вертикальной оси ветряка. Безжалостно отпилил ушки с тяжеловесами и получил «крокозябру» (прекрасно понимаю, что это слово не техническое и даже не литературное, но точнее, по-моему, получившуюся деталь не назовешь) с подшипником по центру. Винтами М4 закрепил ее на отрезке дюралюминиевого уголка 40×40 мм. По центру надо не забыть сделать отверстие, чтобы внутреннее кольцо подшипника не терлось по металлу, к тому же, в него должна входить головка болта, который будет выполнять роль вертикальной оси вращения ветряка.
Легкими ударами молотка (лучше использовать оправку) посадил подшипники горизонтальных осей в трубу. Предварительно закрепил в них сами оси, представляющие собой болты М8х60 мм. Туго затянул гайки, зажав между ними и головками болтов внутренние кольца, ведь если соединение разболтается, подтянуть его будет невозможно, не вынув подшипника. Для установки вертикальной оси ступицы служит отверстие с резьбой М8, сделанное в стенке посередине (по длине) трубы.
Кстати, обратите внимание: подшипники не следует забивать консистентной смазкой — она затруднит вращение, лучше капнуть несколько капель жидкого моторного масла.
Теперь дело за лопастями. Отрезал кусок прямоугольной трубы. С одной стороны прикрепил к нему стабилизатор из листа дюралюминия толщиной 1 мм. Я сделал просто прямоугольники 160×200 мм, но тут можно проявить фантазию. В оригинале, например, стоят стабилизаторы в виде колец. Как мне кажется, они могут быть любой формы, но обязательно симметричными, чтобы не нарушить центр масс лопасти. Винтами М4 закрепил стабилизаторы к лопастям. Оба крыла, разумеется, совершенно одинаковые.
Тайна «скульптуры» кроется в том, что из-за установки стабилизатора на одной из сторон лопасти, ее ось вращения смещается в сторону более тяжелой части (если мы хотим, чтобы лопасть сохраняла произвольное положение в пространстве, а не всегда смотрела стабилизатором вниз). Это очевидно, но такая простейшая асимметрия выглядит очень забавно. И здесь важно точно найти место этой оси. Для этого я зажал в тисках ручку ножа, а на острое лезвие поставил собранную лопасть. Сдвигая ее по долям миллиметра влево-вправо, определил точку равновесия и сделал в ней отверстие диаметром 8 мм под ось. Даже замена одного винтика крепления стабилизатора может нарушить статическую балансировку. А динамическую балансировку я не проводил: непонятно,
как ее выполнить в домашних условиях, да и не нужна она, пожалуй, поскольку обороты здесь невысокие.
Сборка ветряка элементарна. На вертикальную ось устанавливаем дистанционную втулку, накручиваем отрезок нашей трубки-обоймы и затягиваем соединение. На горизонтальные оси надеваем лопасти и притягиваем их гайками. Лучше, если они будут «колпачковые»: с ними законченное изделие выглядит наряднее. Дюралюминиевый уголок закрепляем шурупами на деревянной рейке и устанавливаем ее строго вертикально (вбиваем в землю), воспользовавшись для контроля отвесом. Сечение рейки должно быть таким, чтобы лопасти, встав вертикально, могли свободно описывать вокруг нее круг, поворачиваясь по ветру.
Ну и последний вопрос — он самый интересный, наверное: «Как это все работает!?» По идее, такой ветряк должен сориентироваться по ветру, в горизонтальной и вертикальной плоскостях, — и на этом его движение прекратится. Так в теории и будет, если бы ветер дул постоянно, ровно и в одном направлении. На практике же такое бывает крайне редко. Направление и сила ветра постоянно меняются, пусть и незначительно, а значит, наша скульптура будет находиться в постоянном движении. По горизонтали — за счет стабилизаторов, а лопасти будут крутиться благодаря разности их наветренных площадей с двух сторон асимметрично установленной оси. Во всяком случае, у меня все работает! Даже при слабом ветерке наблюдать за медленными хаотическими движениями лопастей можно бесконечно долго. Неплохой объект для медитации получился. Настраивает мысли на философский лад. А заодно работает у меня на участке в роли необычного. пугала, отлично отгоняющего непрошенных пернатых от посадок.
Источник
Абсолютна гармония искусства с природой: кинетические ветряные скульптуры Энтони Хау
Американский художник Энтони Хау (Anthony Howe) создаёт фантастические кинетические скульптуры, напоминающие инопланетных пришельцев.
После окончания школы живописи и ваяния он занимался написанием пейзажей в своей студии, которая находилась в отдалённом горном районе Нью-Гемпшира.
Пятилетняя идиллия закончилась, когда, по признанию Энтони Хау, ему стало скучно от статических образов, господствующих в искусстве вообще и его творчестве, в частности.
Он переехал в Нью-Йорк, где и увлёкся идеей создания кинетических скульптур.
За 17-летнюю карьеру он стал автором необычных конструкций, которые живут в полной гармонии с природой, вписываются и украшают окружающий пейзаж, движутся то в тихом, то в страстном танце под воздействием ветра и сверкают в лучах восходящего или закатного солнца.
Процесс изготовления начинается с придумывания образа:
Я совершаю длительные прогулки и представляю различные картины и формы.
Самый любимый момент в моей работе – обнаружение абсолютно новой идеи, нового движения.
Затем следует этап проектирования 3D-моделей на компьютере.
Полученный шаблон применяется к металлической заготовке, из которой вырезается криволинейная конфигурация с помощью лазерной резки, дальнейшая обработка металла вполне традиционна.
Кроме нержавеющего металла для создания сюрреалистических скульптур Энтони Хау использует полимеры, стекловолокно, зеркала.
Чтобы проверить устойчивость конструкции при сильном ветре, изобретатель использует забавный способ тестирования.
Я закрепляю скульптуру на своём стареньком Ford F-150 и съезжаю вниз по автостраде
Кинетические ветряные скульптуры, похожие на ожившие иллюстрации научно-фантастических романов, оказывают на зрителя завораживающее воздействие, от феерического зрелища трудно отвести взгляд.
Музей Дизайна предлагает подборку статичных и анимированных изображений из коллекции Энтони Хау,
а также короткие видео о тонко сбалансированных симметричных и ассиметричных композиций, образующих в постоянном движении безупречную трёхмерную гармонию.
Напишите в комментариях о своих впечатлениях!
Источник
Математика во плоти
Что такое кинетическое искусство и как оно работает
Архитектура — застывшая музыка. Это избитое выражение, приписываемое немецкому философу и теоретику искусства Фридриху Шеллингу, касается «большой» архитектуры. Однако с середины XX века художники все больше тяготеют к особым «малым» архитектурным формам — кинетическим скульптурам, которые застывшими назвать уже нельзя. Напротив, эти скульптуры, отдельные элементы которых, взаимодействуя, перемещаются по причудливым траекториям, завораживают зрителя постоянным движением. О кинетических скульптурах пишут книги искусствоведы, спорят посетители выставок. Совместно с Музеем современного искусства «Гараж» мы попытаемся взглянуть на них под другим углом — глазами математика.
С 17 марта по 9 мая в Музее современного искусства «Гараж» проходит «Трансатлантическая альтернатива» — первая в России крупная выставка, посвященная кинетическому и оптическому искусству Восточной Европы и Латинской Америки. На ней экспонируется более сотни произведений искусства 1950–1970-х годов, в том числе кинетические скульптуры, картины, рисунки, видео и инсталляции, а также уникальные архивные материалы. Логическим продолжением выставки «Трансатлантическая альтернатива» будет открытие «Атома» Вячеслава Колейчука — реконструкции монументальной цветодинамической скульптуры, стоявшей у истоков кинетического искусства в России. Мы решили разобраться, как устроен «Атом» и другие кинетические скульптуры.
Александр Колдер (Alexander Calder)
Американский скульптор (1898–1976), в начале 1930-х годов обратился к изготовлению динамических конструкций — так называемых «мобилей». Первые «мобили» Колдера приводились в движение моторами, но впоследствии, стремясь к созданию динамических систем, способных отражать постоянную изменчивость природы, Колдер перешел к «естественным» способам динамизации формы, а именно к конструкциям с неустойчивым равновесием, способным приходить в движение от малейшего колебания воздуха.
В своих работах Колдер использовал механизмы на основе рычажных весов — вращающиеся под действием потоков воздуха конструкции из проволоки и металла. К созданию таких «мобилей» применить классическую механику и математику довольно сложно, поскольку каждый из них состоит из большого числа частей совершенно разной формы. Скорее всего, параметры элементов скульптур — плоских грузиков разнообразной формы, расположенных иерархически, — определялись опытным путем, поскольку первую свою скульптуру Александр Колдер построил еще в 1930-х годах. Кстати, многие историки искусства считают, что он был первым, кто определил контуры «мобильного» направления кинетического искусства.
Впрочем, в настоящее время для разработки подобных конструкций можно использовать компьютер и метод конечных элементов, когда виртуальную модель разбивают на отдельные очень маленькие элементы, к которым применяют известные простые физико-математические законы и правила — правило равновесия рычага, правило нахождения центра тяжести плоской фигуры и так далее. Например, центр тяжести кольцевого сектора, который встречается в работах Колдера, рассчитывается по следующей формуле:
Часто повторяющийся у Колдера мотив — сложно устроенные и вложенные друг в друга «весы». Мобили, построенные по этому принципу, породили множество подражаний, а в интернете даже появляются инструкции, как сделать такой мобиль своими руками, без привлечения сложных вычислений:
Тео Янсен (Theo Jansen)
Нидерландский художник (родился в 1948 году), известен своими «искусственными формами жизни» — скелетообразными фигурами, способными передвигаться по песчаным пляжам под воздействием силы ветра. Генетические алгоритмы Янсена способны симулировать биологическую эволюцию видов.
В работах Тео Янсена находят применение идеи стопоходящей машины, основной узел которой переводит вращательное движение в поступательное. Скульптуры Янсена напоминают причудливые существа, которые ловко перебирают десятками ног и с легкостью движутся под действием ветра. Сам художник называет их «пляжными зверями», Strandbeest. Однако в действительности научить «зверей» ходить не спотыкаясь не так-то просто — необходимо не только корректно спроектировать каждую ногу, но и организовать их совместную работу. Для этого скульптору нужно решить систему нелинейных алгебраических уравнений, вытекающих из теоремы Пифагора.
Вот конкретный пример. Рассмотрим два рычага 1 и 2, соединенных шарниром в точке 5. Допустим, нам известны координаты концов 3 и 4 и мы хотим найти положение шарнира. Для решения этой задачи необходимо аналитически или численно решить систему двух нелинейных алгебраических уравнений, где L1 и L2 — это гипотенузы двух прямоугольных треугольников (длины рычагов), а x4 − x5, y4 − y5, x3 − y5 и y3 − y5 — это длины катетов. Как известно, эти величины связывает между собой теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Разумеется, каждая «нога» содержит больше двух шарниров, а потому задача, которую предстоит решить художнику перед постройкой скульптуры, гораздо сложнее. Так или иначе, она сводится к оптимизации узлов — то есть подбору таких длин рычагов, при которых конструкция будет двигаться плавно, без толчков. Наконец, после того как скульптура будет спроектирована, необходимо сделать оптимизационные прочностные расчеты и убедиться в том, что она не сломается. Тут пригодятся знания, которые аккумулирует легендарная наука под названием сопротивление материалов (или, как ее сокращенно называют студенты, «сопромат»). И только после проведения всех расчетов скульптор может браться за инструменты, чтобы собрать конструкцию из пластиковых трубочек, деревянных брусков, скотча и полиэтилена.
Кстати, первым человеком, который стал применять высшую математику для проектирования подобных конструкций, был наш соотечественник Пафнутий Чебышёв, стопоходящая машина которого получила золотую медаль на Всемирной выставке в Париже в 1878 году и сейчас хранится в Политехническом музее в Москве. Впрочем, механические «звери» Тео Янсена ушли гораздо дальше — они запасают энергию ветра, надувая упругий «желудок», состоящий из пластиковых бутылок, умеют определять тип почвы, по которой ходят, и выбрасывают якоря, если ветер дует слишком сильно. Все это удается им без привлечения сложной электроники.
Лимэн Уитакер (Lyman Whitaker)
Американский художник, чья творческая биография насчитывает уже более пятидесяти лет. Последние тридцать лет он посвящает свои усилия «ветряным скульптурам» (Wind Sculptures).
Тогда как «мобили» Александра Колдера нужно демонстрировать в закрытом помещении, работы Лимэна Уитакера требуют дуновения ветра, от которого они начинают вращаться и создавать нужный «эстетический» эффект. В его работах используются законы аэродинамики, а сами скульптуры представляют собой своеобразные приборы для замера скорости ветра (анемометры, ветромеры).
Скорее всего, на создание мобилей Уитакера натолкнуло вращение традиционного флюгера с анемометром в виде четырех полусфер, которые используют метеорологи. Впрочем, сам автор утверждает, что черпает вдохновение в природе — в раскачивании травы и деревьев под действием ветра. Современные компьютерные программы позволяют моделировать геометрию обтекания газом или жидкостью сложных статичных или подвижных конструкций, однако Уитакер работает «по наитию», определяя профили каждого из «мельничных крыльев» опытным путем.
Обтекание тела воздухом описывается законом сохранения энергии — потенциальная энергия переходит в кинетическую и обратно, но сумма энергий остается постоянной. В газодинамике потенциальная энергия определяется давлением потока, а кинетическая — скоростью потока. Вместе их связывает формула, открытая Даниилом Бернулли в начале XVIII века. На рисунке видно, что скорость потока воздуха над крылом выше скорости потока под крылом.
Перепад давлений под крылом и уравнение Бернулли
Источник