- Развертка многогранника для склеивания. Развертка звездчатого многогранника
- Красивая геометрия
- Разные грани — разные формы
- Самый первый многогранник – кубик
- Занимательные грани
- Правильные и неправильные звездчатые многогранники
- Красота в простоте
- Как построить развертку самостоятельно?
- Тонкости работы
- Звездчатый многогранник своими руками
- Многогранник Икосаэдр из бумаги. Kusudama by Mitsunobu Sonobe
- Малый звёздчатый додекаэдр из картона.
- 100 символов России на одной картинке
- Как сделать ромбододекаэдр
- Кубооктаэдр из картона
- Усечённый октаэдр из картона.
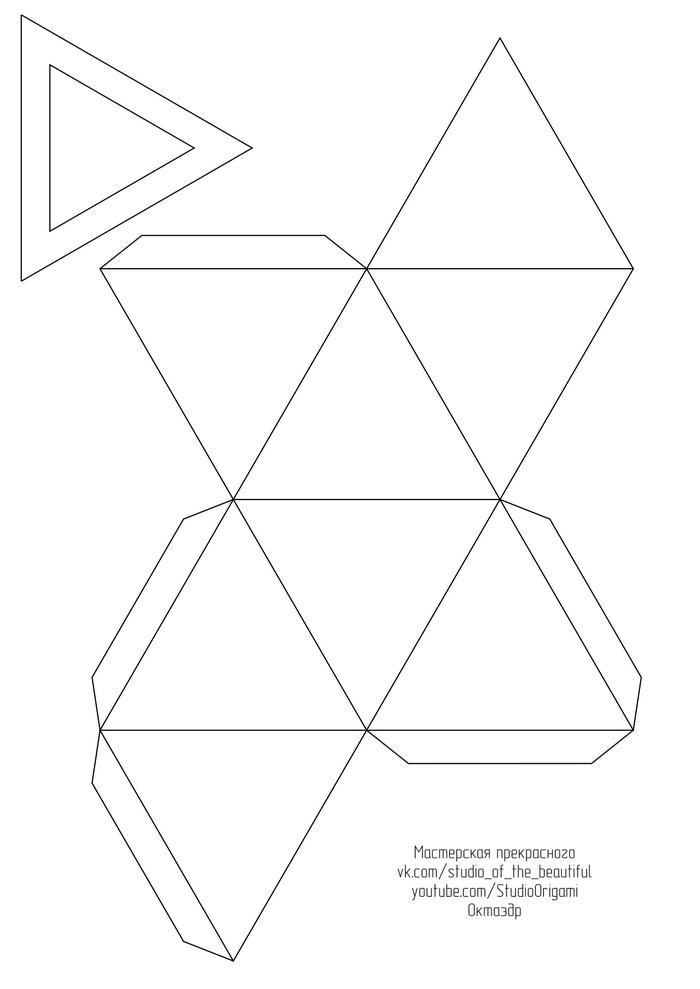
- Как сделать октаэдр
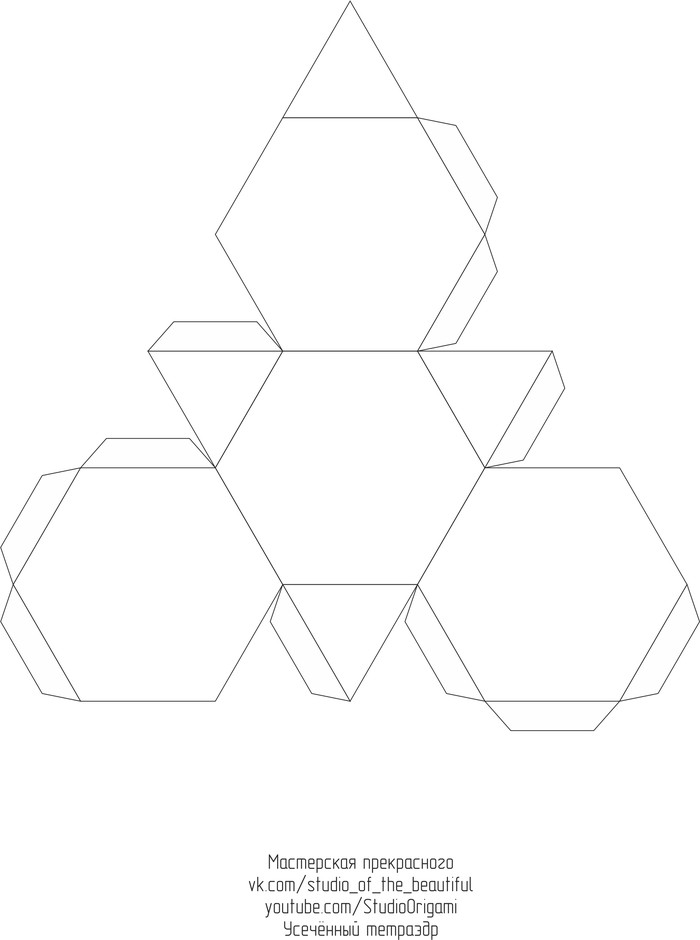
- Усечённый тетраэдр из картона
- Как сделать квадратную пирамиду
Развертка многогранника для склеивания. Развертка звездчатого многогранника
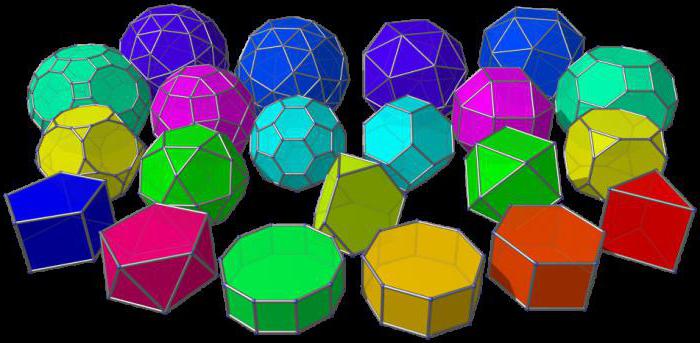
Много интересного можно найти для себя в тех сферах науки, которые, казалось бы, никогда не пригодятся в привычной жизни простого обывателя. Например, геометрия, о которой большинство забывают, только лишь переступив порог школы. Но странным образом малознакомые области науки становятся очень увлекательными, если с ними столкнуться поближе. Вот и геометрическая развертка многогранника – совершенно ненужная в повседневной жизни вещь – может стать началом увлекательного творчества, способного захватить и детей, и взрослых.
Красивая геометрия
Украшать интерьер дома, создавая своими руками необычные, стильные вещи, – это увлекательное творчество. Смастерить самостоятельно из плотной бумаги различные многогранники – значит создать уникальные вещи, которые могут стать просто занятием на день или два, а могут превратиться в дизайнерские интерьерные украшения. К тому же с развитием техники, способной к пространственному моделированию всевозможных вещей, стало возможным создание стильных и современных 3D-моделей. Есть мастера, которые при помощи простроения разверток по законам геометрии делают из бумаги макеты животных и различных предметов. Но это достаточно сложное математическое и чертежное творчество. Начать работать в подобной технике поможет развертка многогранника.
Разные грани — разные формы
Многогранники – это особая сфера геометрии. Они бывают простые – к примеру кубики, которыми дети играют с раннего возраста, – а бывают очень и очень сложные. Простроение развертки многогранников для склеивания считается достаточно сложной областью конструирования и творчества: нужно не только знать основы черчения, геометрические особенности пространства, но и иметь пространственное воображение, позволяющее оценить правильность решения еще на стадии проектирования. Но и одной фантазией не обойтись. Чтобы сделать развертки многогранников из бумаги, не достаточно просто представить, как в конце концов должна выглядеть работа. Нужно уметь правильно ее просчитать, сконструировать, а также грамотно начертить.
Самый первый многогранник – кубик
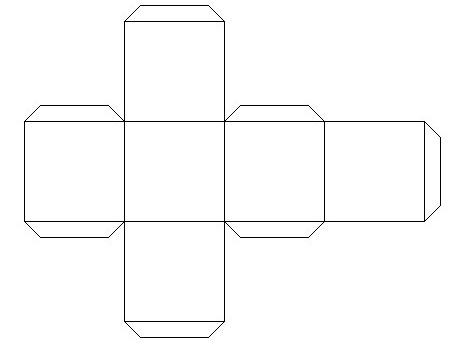
Скорее всего, каждый человек, посещавший школу, еще в начальных классах сталкивался на уроках труда с работой, результатом которой должен был стать бумажный кубик. Чаще всего учительница раздавала заготовки – развертки многогранника куба на плотной бумаге со специальными кармашками, предназначенными для склеивания граней модели в единое целое. Такой работой ученики начальной школы могли гордиться, ведь при помощи бумаги, ножниц, клея и своих усилий получалась интересная поделка – трехмерный куб.
Занимательные грани
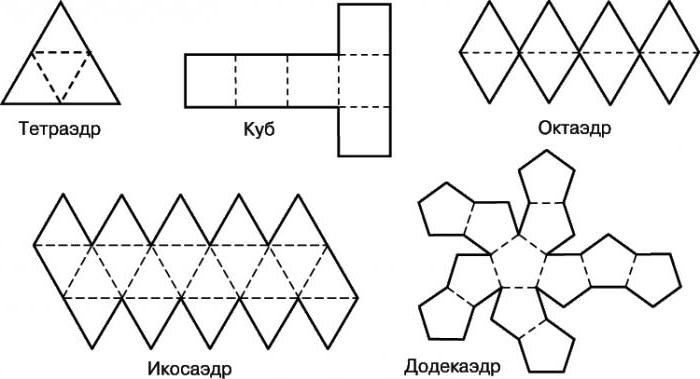
Удивительно, но многие знания об окружающем мире становятся интересны не на школьной скамье, а лишь тогда, когда можно найти в них нечто увлекательное, способное дать что-то новое, необычное в привычной жизни. Не многие взрослые помнят, что те же многогранники делятся на огромное количество видов и подвидов. Например, есть так называемые платоновы тела – выпуклые многогранники, состоящие только лишь из правильных многоугольников. Таких тел всего пять: тетраэдр, октаэдр, гексаэдр (куб), икосаэдр, додекаэдр. Они представляют собой выпуклые фигуры без впадин. Звездчатые многогранники состоят из этих основных фигур в различных конфигурациях. Поэтому-то развертка многогранника простого позволяет нарисовать, вернее начерить, а затем и склеить из бумаги звездчатый многогранник.
Правильные и неправильные звездчатые многогранники
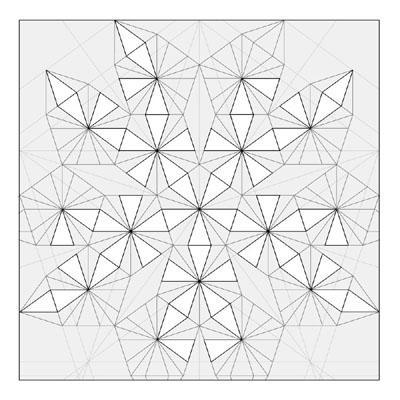
Складывая платоновые тела между собой в определенном порядке, вы можете построить немало звездчатых многоранников – красивых, сложных, многокомпонентных. Но они будут называться «неправильными звездчатыми многогранниками». Правильных звездчатых многогранников всего четыре: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Развертки многогранников для склеивания не будут простыми чертежами. Они, как и фигуры, будут состоять из нескольких компонентов. Так, например, малый звездчатый додекаэдр строится из 12 пятиугольных равнобочных пирамид, сложенных по типу правильного додекаэдра. То есть для начала придется начертить и склеить 12 одинаковых штук правильных пирамид, состоящих из 5 равных граней. И только затем из них можно сложить звездчатый многогранник. Развертка самого малого звездчатого додекаэра – сложное и практически невыполнимое задание. Чтобы ее простроить, нужно суметь на одной плоскости уместить соединенные друг с другом 13 разверток разных геометрических объемных тел.
Красота в простоте
Все объемные тела, построенные по законам геометрии, будут смотреться завораживающе, в том числе и звездчатый многогранник. Развертка каждого элемента любого подобного тела должна быть выполнена максимально точно. И даже самые простые объемные многогранники, начиная с платонового тетраэдра, – удивительная красота гармонии мироздания и труда человека, воплощенного в бумажной модели. Вот, допустим, самый многогранный из платоновых выпуклых многогранников – додекаэдр. В этой геометрической фигуре 12 абсолютно одинаковых граней, 30 ребер и 12 вершин.Чтобы сделать развертки правильных многогранников для склеивания, нужно приложить максимум аккуратности и внимательности. И чем крупнее фигура по размерам, тем точнее должны быть все измерения.
Как построить развертку самостоятельно?
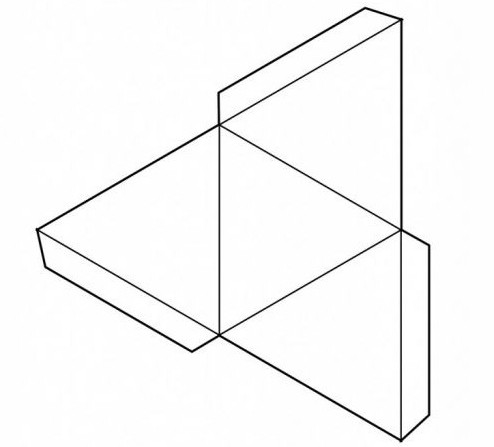
Пожалуй, помимо склеивания многогранника – хоть звездчатого, хоть платоновского, – еще интереснее построить развертку будущей модели собственными силами, оценив свои способности к черчению, конструированию и пространственному вообжению. Простые платоновсткие тела состоят из простых многоугольников, которые в одной фигуре идентичны друг другу. Так, тетраэдр – это три равнобедренных треугольника. Прежде чем простроить развертку, нужно представить себе, как правильно сложить плоские многоугольники между собой, чтобы получить многогранник. Треугольники можно соединить между собой по ребрам, прочертив один рядом с другим. Для склеивания развертки многогранников схемы должны быть снабжены специальными кармашками или клапанами, которые позволят соединить все части в единое целое. Тетраэдр – простейшая фигура из четырех граней. Октаэдр можно представить как двойной тетраэдр, у него восемь гарней – равнобедренных треугольников. Гексаэдром называют знакомый всем с детства куб. Икосаэдр представляет собой соединение 20 равнобедренных треугольников в правильный выпуклый многогранник. Додекаэдр – это объемная фигура из 12 граней, каждая из которых представляет собой правильный пятиугольник.
Тонкости работы
Построить разверту многогранника и склеить из нее бумажную модель – дело тонкое. Развертку, конечно, можно взять уже готовую. А можно, приложив услилия, построить ее самостоятельно. Но чтобы сделать полноценную объемную модель многогранника, нужно ее собрать. Многогранник лучше всего делать из плотной бумаги, которая хорошо держит форму и не коробится от клея. Все линии, которые необходимо согнуть, лучше всего предварительно продавить, используя, например, непишущую шариковую ручку или обратную сторону лезвия ножа. Этот нюанс поможет сложить модель аккуратнее, с соблюдением размеров и направлений ребер.
Если сделать разные многогранники из цветной бумаги, то такие модели можно использовать в качестве декоративных элементов, украшающих помещение – детскую комнату, кабинет, гостиную. Кстати, многогранники можно назвать уникальной находкой декораторов. Современные материалы позволяют на основе геометрических фигур создавать оригинальные предметы интерьера.
Источник
Звездчатый многогранник своими руками
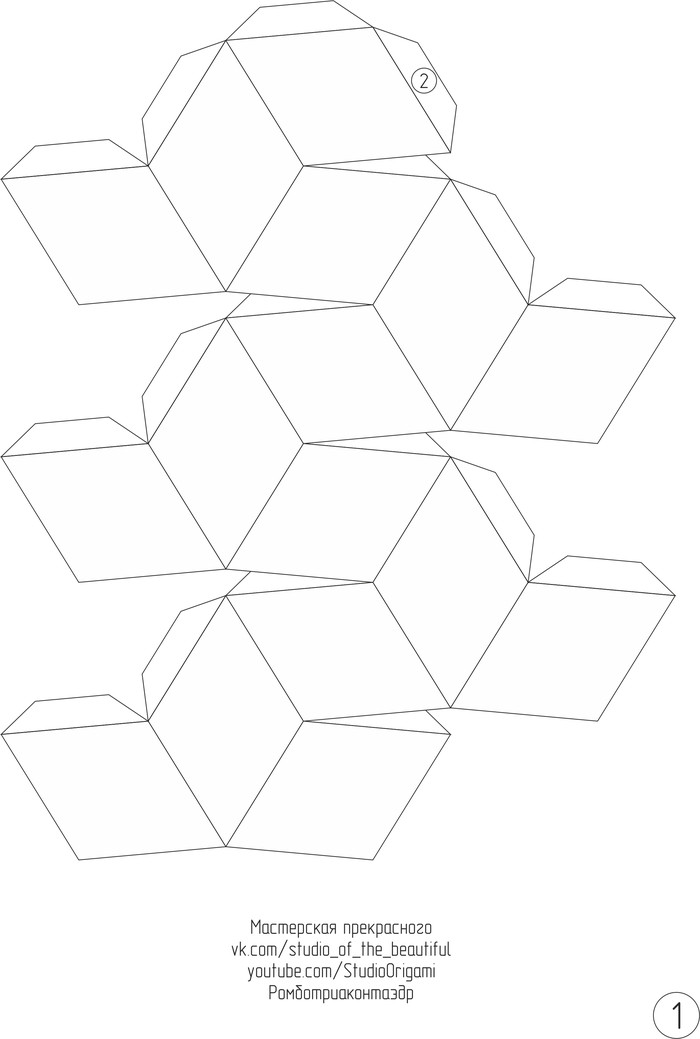
Представляю Вам новую свою схему и видеоинструкцию по сборке одного из Каталановых тел* — ромботриаконтаэдра. Но для начала немного описания многогранника.
Ромботриаконтаэдр — это выпуклый тридцатигранник с одинаковыми ромбическими гранями. Он состоит из 30 граней (золотых ромбов**), 32 вершин и 60 рёбер. Является двойственным по отношению к икосододекаэдру.
*Каталановы тела — это выпуклые многогранники, обладающие двумя свойствами:
1. Все грани одинаковые, но не являются правильными многоугольниками;
2. Многогранник относится к одному из трёх существующих типов пространственной симметрии.
Эти многогранники названы в честь бельгийского математика Эжена Каталана, который впервые описал их в 1865 году.
**Золотой ромб — это ромб, чьи диагонали относятся друг к другу как φ (золотое сечение, равное примерно 1,618).
Использование ромботриаконтаэдра в мире:
Тридцатигранные игральные кости.
Игрушка Ball of Whacks от Роджера фон Эйк.
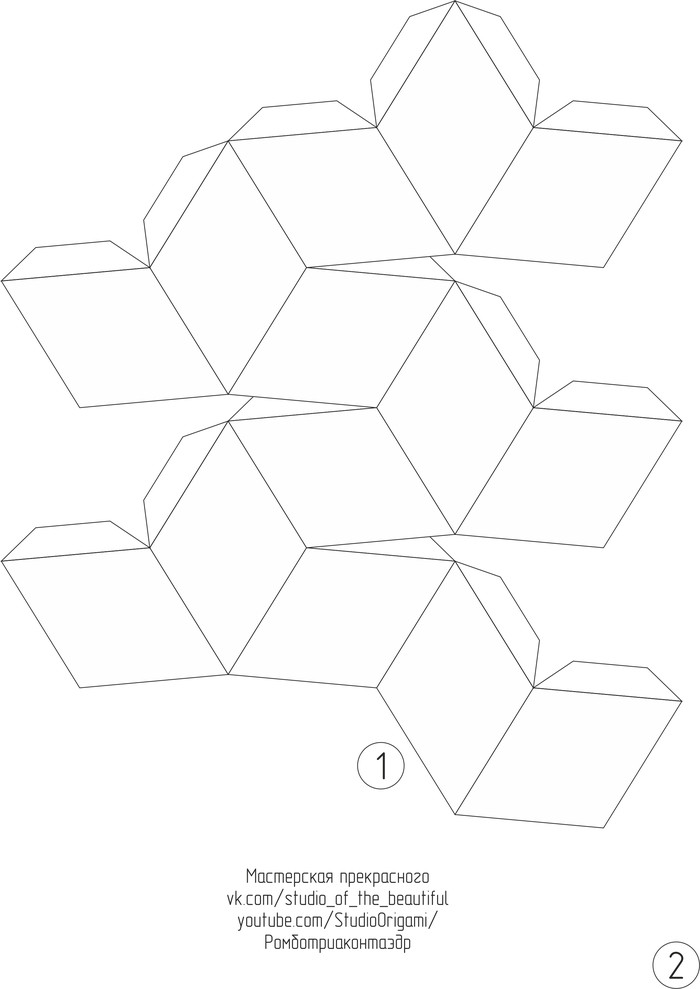
А теперь сама инструкция для сборки. Для развёртки ромботриаконтаэдра необходимо 2 листа цветного картона формата А4. Длина ребра у многогранника — 3,8 см, а высота многогранника — 10,5 см. Развёртка ромботриаконтаэдра в формате pdf или изображениями ниже:
Ниже представлена видеоинструкция по сборке ромботриаконтаэдра:
Также смотрите предыдущие мои посты про многогранники:
Многогранник Икосаэдр из бумаги. Kusudama by Mitsunobu Sonobe
Многогранник Икосаэдр — замечательная и интересная оригами поделка из бумаги, которая станет подарком для ценящих людей. Такой многогранник — кусудаму можно использовать как елочное украшение на Новый год в качестве игрушки. Для создания многогранника понадобиться 30 квадратных листов бумаги. Размер одного листа 8*8 см. Designed by: Mitsunobu Sonobe
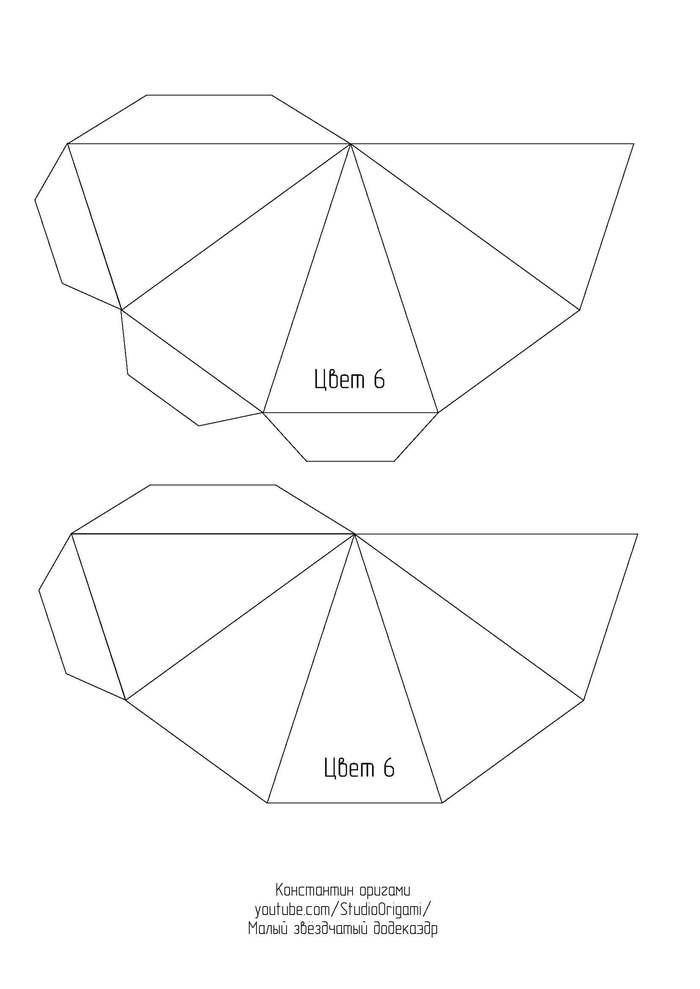
Малый звёздчатый додекаэдр из картона.
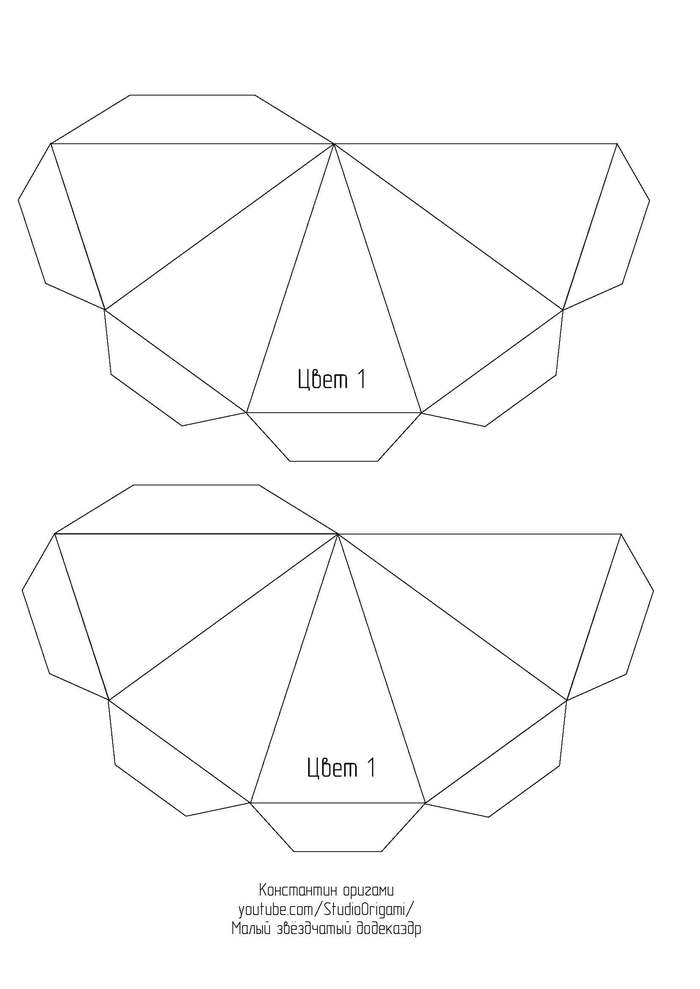
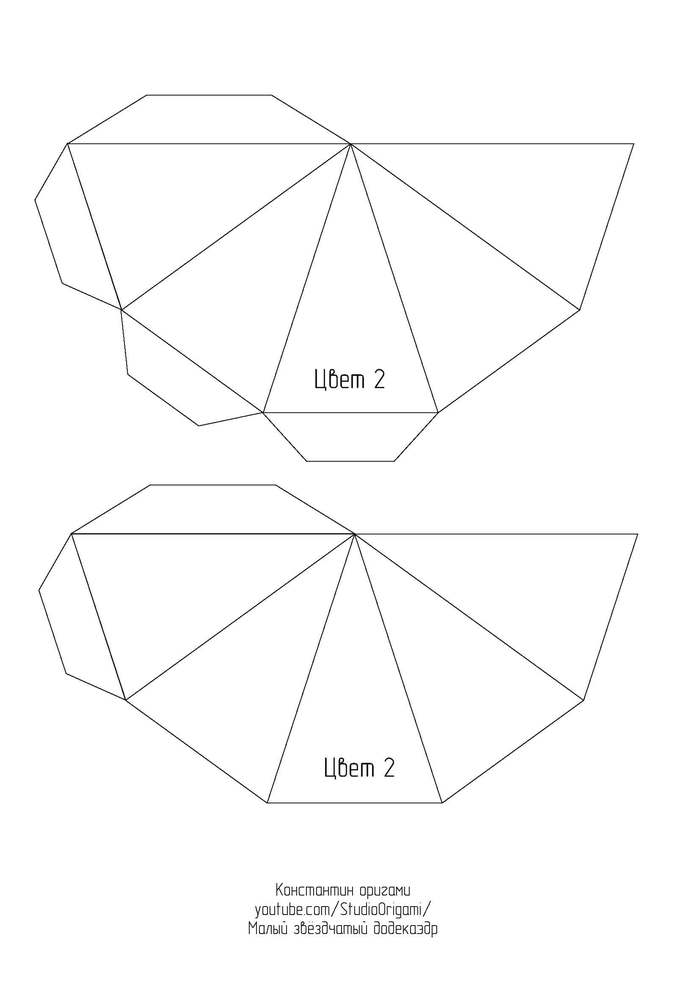
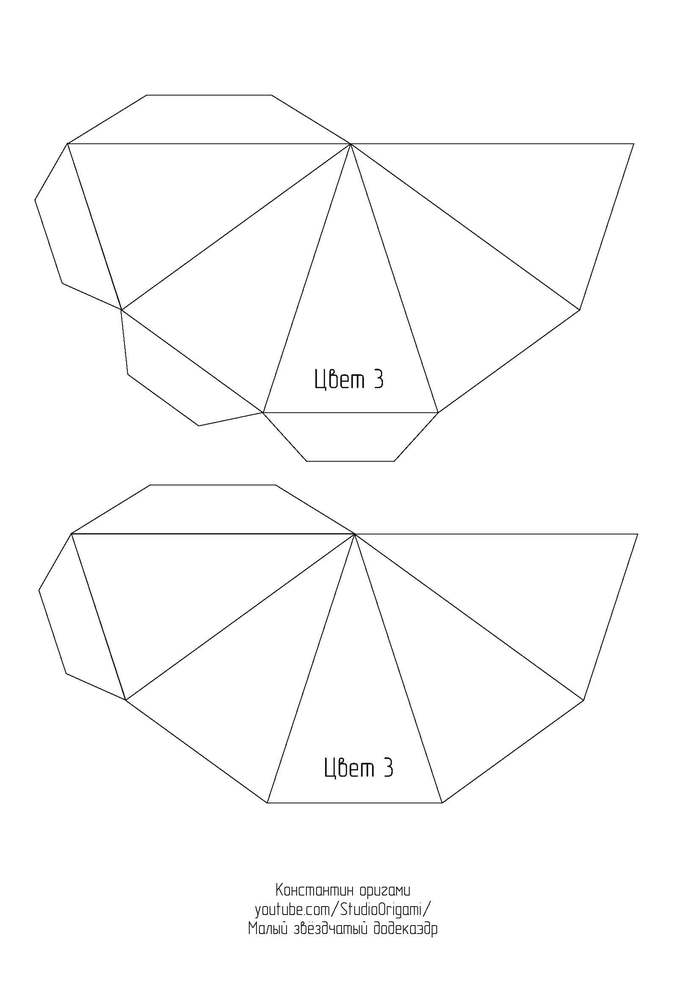
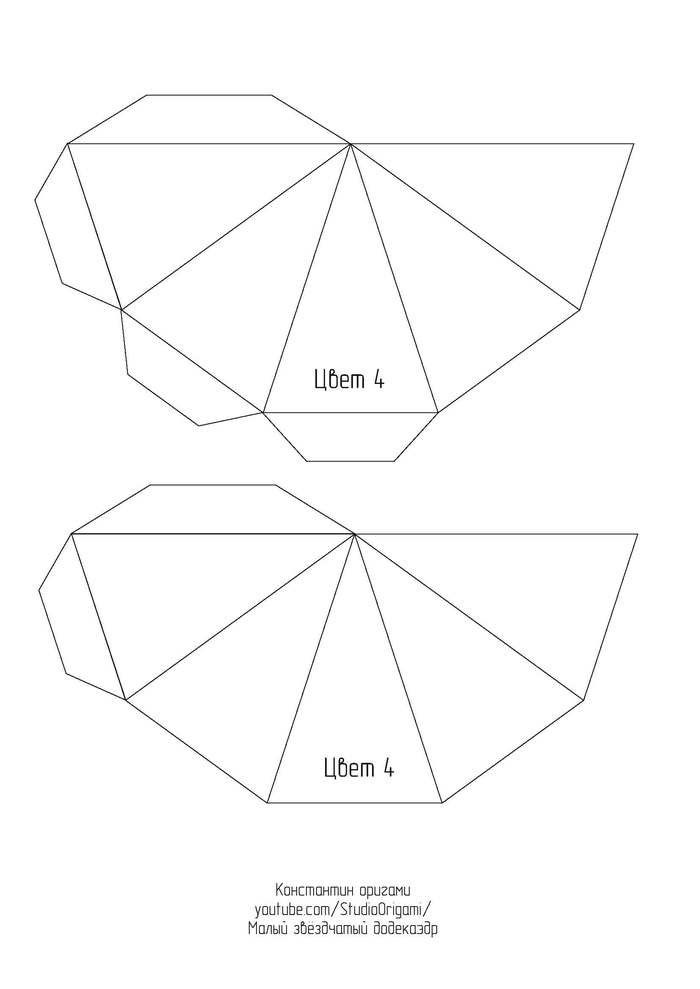
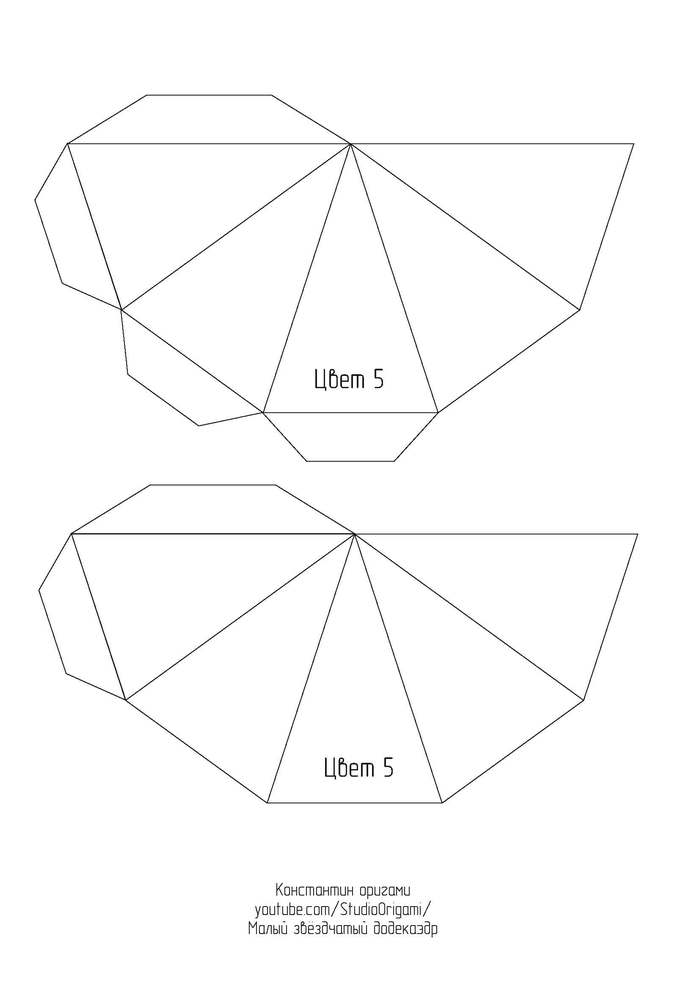
Представляю Вам новую свою схему и видеоинструкцию по сборке одного из тел Кеплера-Пуансо* — малого звёздчатого додекаэдра.
Малый звёздчатый додекаэдр является одним из четырёх невыпуклых правильных многогранников. Он состоит из 12 граней в виде пентаграмм с пятью пентаграммами, сходящимися в каждой вершине. Он имеет то же самое расположение вершин, что и выпуклый правильный икосаэдр. Кроме того, у него то же самое расположение рёбер, что и у большого икосаэдра. Этот многогранник считается первой звёздчатой формой додекаэдра.
*Тело Кеплера-Пуансо — это тело, представляющее собой правильный звёздчатый многогранник, не являющийся соединением платоновых и звёздчатых тел.
Для развёртки малого звёздчатого додекаэдра необходимо 6 листов цветного картона формата А4. Длина ребра получается 8 см, а высота многогранника — около 25 см. Ссылка на развёртку в формате pdf или картинками ниже:
Также смотрите видеоинструкцию по сборке многогранника:
Если понравилось, то смотрите предыдущие мои посты про многогранники:
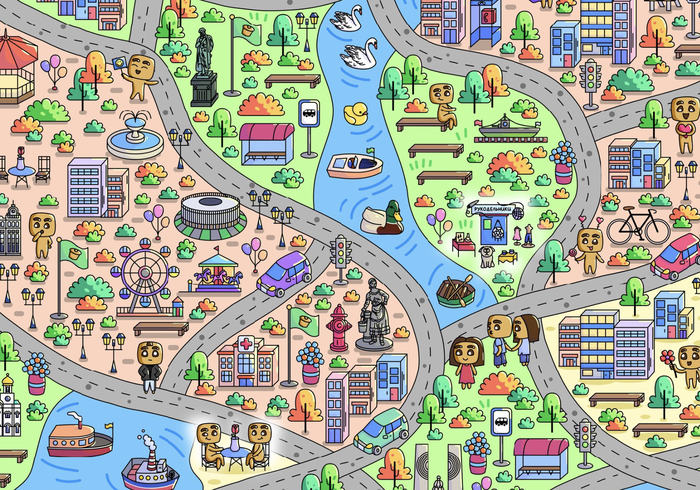
100 символов России на одной картинке
Мы на Пикабу сделали огромную карту-виммельбух (на скрине только кусочек!) с 20 городами России и их достопримечательностями.
Здания, памятники, арт-объекты — по карте можно немного узнать про каждый город. А еще мы спрятали кучу забавных пасхалок и отсылок к массовой культуре. Тут и расщепленная Таносом Печенька, и Свидетель из Фрязино, и еще куча всего.
А самые внимательные получат награду в профиль и призы от Пикабу!
Как сделать ромбододекаэдр
Ромбододекаэдр (Rhombic Dodecahedron) — это двенадцатигранник, составленный из одинаковых ромбов. У ромбододекаэдра 14 вершин и 24 ребра. Ромбододекаэдр является каталановым многогранником. Двойственным многогранником ромбододекаэдра является кубооктаэдр.
Каталановы многогранники — это выпуклые многогранники, обладающие двумя свойствами:
1. Все грани одинаковые, но не являются правильными многоугольниками;
2. Многогранник относится к одному из трёх существующих типов пространственной симметрии (тетраэдрический, октаэдрический или икосаэдрический).
Эти многогранники названы в честь бельгийского математика Эжена Каталана, который впервые описал их в 1865 году.
Где встречается ромбододекаэдр:
Головоломка наподобие кубика Рубика.
Капелла Гранато в долине Циллерталь (Австрия).
А теперь сама инструкция для сборки. Для развёртки ромбододекаэдра необходимо 2 листа двухстороннего цветного картона формата А4 (или плотной бумаги). Длина ребра у ромбододекаэдра — 6,1 см. Развёртку многогранника в формате pdf вы можете скачать по ссылке. Если у Вас нет принтера, то Вы можете сами нарисовать развёртку ромбододекаэдра с помощью линейки и карандаша, смотря видеоинструкцию ниже:
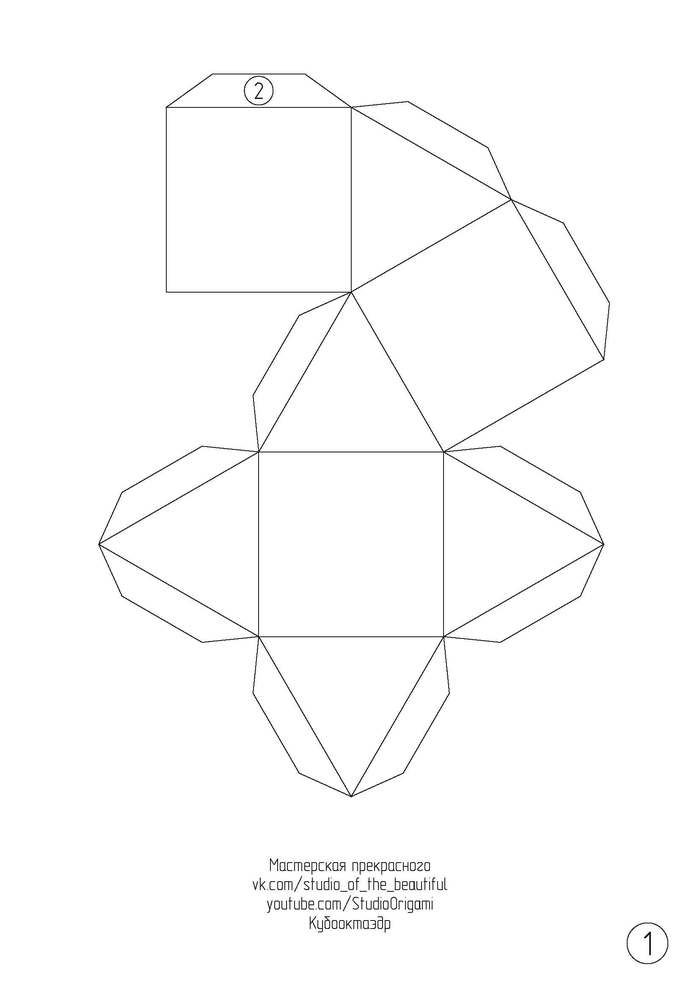
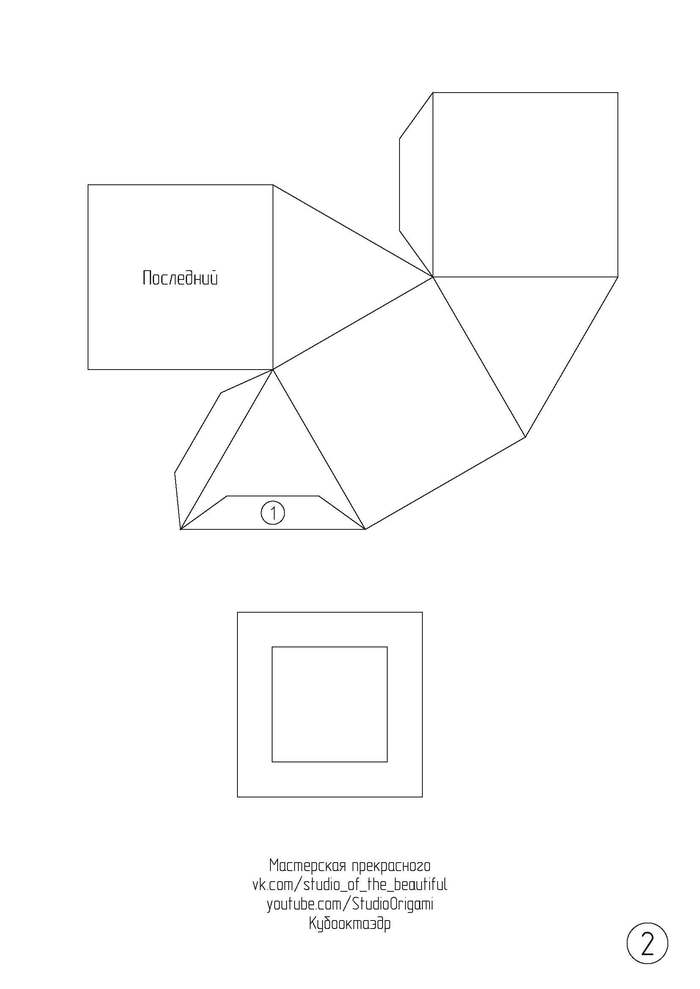
Кубооктаэдр из картона
Представляю Вам новую свою схему и видеоинструкцию по сборке одного из Архимедовых тел* — кубооктаэдра. Но в начале, как обычно, немного описания многогранника.
Кубооктаэдр (кубоктаэдр) — это полуправильный многогранник, состоящий из 14 граней (8 правильных треугольников и 6 квадратов). В кубооктаэдре 12 одинаковых вершин, в которых сходятся два треугольника и два квадрата, а также 24 одинаковых ребра, каждое из которых разделяет треугольник и квадрат. Двойственный к кубооктаэдру многогранник — ромбододекаэдр.
*Архимедовы тела — это выпуклые многогранники, обладающие двумя свойствами:
1. Все грани являются правильными многоугольниками двух или более типов;
2. Многогранник относится к одному из трёх существующих типов пространственной симметрии.
Использование кубооктаэдра в мире:
Головоломка наподобие кубика Рубика.
Игрушка Geo Twister.
Памятники в Императорском дворе Шугакуин (Япония)
Весак Куду — традиционные фонари, которые ежегодно делают на Шри-Ланке в честь праздника Весак, обычно имеют кубооктаэдрическую форму.
Четырнадцатигранные игральные кости.
Кубооктаэдр даже засветился в Звёздном Пути (оригинальный сериал — сезон 2, серия 22).
А теперь сама инструкция для сборки. Для развёртки кубооктаэдра необходимо 2 листа цветного картона формата А4 (или плотной бумаги). Длина ребра у многогранника — 5,4 см, а высота многогранника — 7,5 см. Развёртка кубооктаэдра в формате pdf или изображениями ниже:
Ниже представлена видеоинструкция по сборке кубооктаэдра:
Также смотрите мой предыдущий мои пост про многогранники из картона:
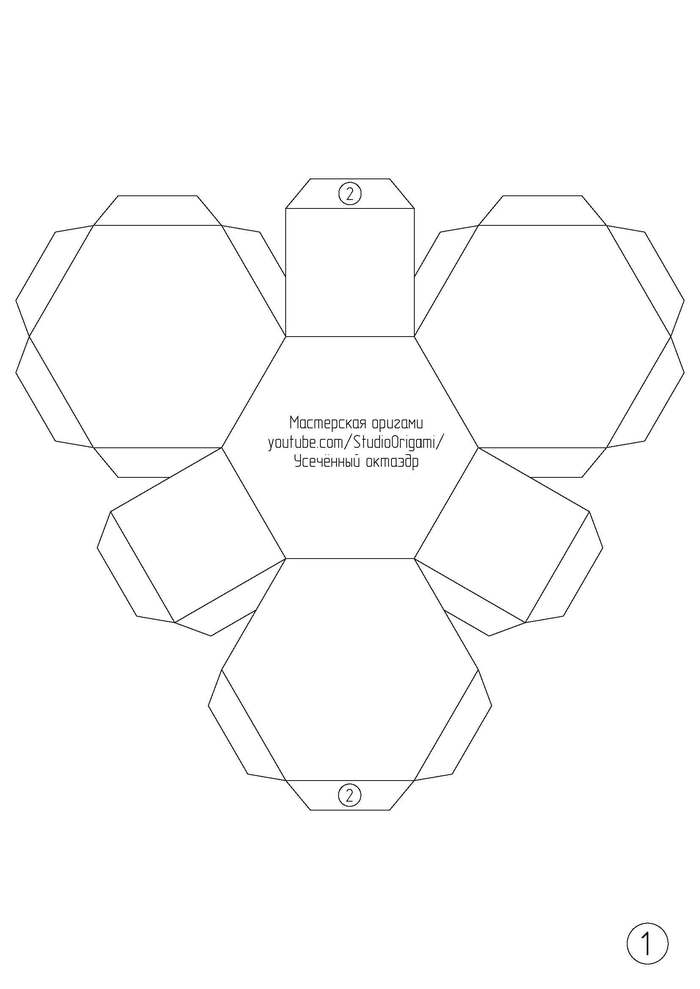
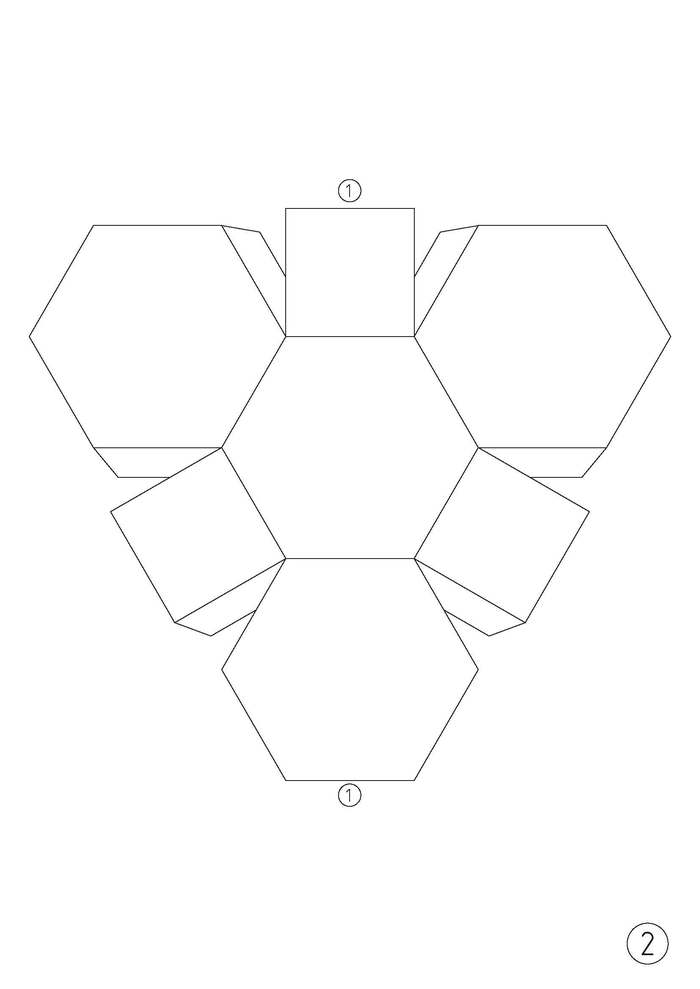
Усечённый октаэдр из картона.
Представляю Вам свою схему и видеоинструкцию по сборке одного из Архимедовых тел — усечённого октаэдра.
Усечённый октаэдр — полуправильный многогранник, состоящий из 14 граней (8 правильных шестиугольников и 6 квадратов). В усечённом октаэдре 24 одинаковых вершины, в каждой из которых сходятся два шестиугольника и квадрат, а также 24 ребра, каждое из которых разделяет шестиугольник и квадрат, и 12 рёбер, каждое из которых разделяет два шестиугольника.
Для развёртки усечённого октаэдра необходимо 2 листа цветного картона формата А4. Сама развёртка многогранника представлена в виде картинки ниже, или по ссылке в формате pdf.
Если Вам что-то непонятно при сборке многогранника, то можете посмотреть мою видеоинструкцию:
Ещё можете посмотреть мои видеоинструкции про другие многогранники:
Как сделать октаэдр
Октаэдр (квадратная бипирамида, восьмигранник) — многогранник, гранями которого являются восемь правильных треугольника. Октаэдр является одним из пяти правильных многогранников (Платоновы тела). У октаэдра 8 граней, 6 вершины и 12 рёбер. Двойственным многогранником октаэдра является гексаэдр (куб).
Правильный многогранник — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий одной из пространственной симметрией. У октаэдра октаэдрическая симметрия.
Где встречается октаэдр:
Головоломка Октаэдр Трайбера
Восьмигранные игральные кости.
Игра Octahedron от Demimonde.
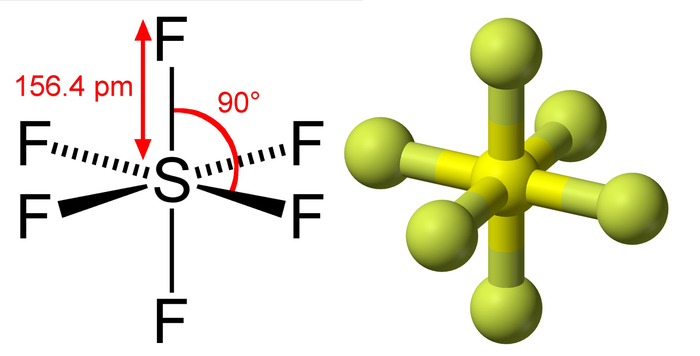
Молекулярная структура Фторида серы(VI).
Террариум для растений.
Монолит Мортиса из Звёздных Войн: Войны Клонов (3 сезон, 15 серия).
Корабль королевы Борг из Звёздного Пути: Вояджер (5 сезон 15/16 серия)
А теперь сама инструкция для сборки. Для развёртки октаэдра необходим лист двухстороннего цветного картона формата А4. Длина ребра у октаэдра получается 8 см. Развёртку октаэдра в формате pdf Вы можете скачать по ссылке или картинкой ниже:
Если у Вас нет принтера, то Вы можете сами нарисовать развёртку октаэдра с помощью линейки и циркуля, смотря видеоинструкцию ниже:
Усечённый тетраэдр из картона
Представляю Вам новую свою схему и видеоинструкцию по сборке одного из Архимедовых тел* — усечённого тетраэдра.
Усеченный тетраэдр — это выпуклый многогранник, состоящий из 8 граней (4 правильных шестиугольников и 4 равносторонних треугольников), 12 вершин и 18 рёбер. Его можно построить, обрезав все 4 вершины правильного тетраэдра на треть от первоначальной длины ребра.
*Архимедовы тела — это выпуклые многогранники, обладающие двумя свойствами:
1. Все грани являются правильными многоугольниками двух или более типов;
2. Многогранник относится к одному из трёх существующих типов пространственной симметрии (для усечённого тетраэдра двойственным многогранником является триакистетраэдр).
Для развёртки усечённого тетраэдра необходим 1 лист цветного картона формата А4. Длина ребра у многогранника — 3,5 см, а высота многогранника — 5 см. Развертка усечённого тетраэдра в формате pdf или изображением ниже:
Смотрите видеоинструкцию по сборке усечённого тетраэдра:
Если понравилось, то смотрите предыдущие мои посты про многогранники:
Как сделать квадратную пирамиду
Представляю видеоинструкцию по сборке квадратной пирамиды.
Квадратная пирамида — это пирамида, имеющая квадратное основание. Квадратная пирамида состоит из 5 граней (4 треугольников и 1 квадрата), 5 вершин, 8 рёбер.
Пирамида — это многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину. Данная пирамида также является одним из тел Джонсона. Тело Джонсона (правильногранный многогранник) — это выпуклый многогранник, каждая грань которого является правильным многоугольником, при этом многогранник не должен является ни платоновым телом, ни архимедовым, ни призмой, ни антипризмой.
Квадратная пирамида много где встречается в мире:
Источник